Project Euler——Problem 21

daybreakcx posted @ 2009年7月22日 05:10 in Prject Euler , 1064 阅读

原题与答案：

Problem 21

05 July 2002

Let d(n) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n).
If d(a) = b and d(b) = a, where a 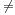$\neq$ b, then a and b are an amicable pair and each of a and b are called amicable numbers.

For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.

Evaluate the sum of all the amicable numbers under 10000.

Answer:31626

分析与解答：

这个题目的意思是求10000内所有的相亲数的和，所谓的相亲数是指对于一对自然数，如果他们的小于本身的约数的和（不包括本身）等于对方的话，他们称为一对相亲数。这个题目可以通过枚举获得，其实实际上相亲数的数量非常少，首次做这个题的时候我是通过直接到网上查找获得的结果，而如果要写程序实现的话只要枚举10000以内的数值就可以一对对判断了。求所有约数的和可以先将原来的数值分解成如下形式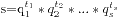： $s=q_1^{t_1}*q_2^{t_2}*...*q_s^{t_s}$ ，实际上获得所有约数的和就是将所有的 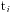t_i 从0开始到本身进行枚举，然后将所有的枚举情况都加起来。假设其他的指数都不变的情况下，那么就相当于将其他确定的因数构成的元素看成一体当作公约数提取，本身这项就是形成了一个等比数列，因此我们要求的所有约数的和就是 $\dfrac{q_1^{t_1+1}-1}{q_1-1}*\dfrac{q_2^{t_2+1}-1}{q_2-1}*...*\dfrac{q_s^{t_s+1}-1}{q_s-1}$ ，最后减去本身就是所有小于本身的约数的和了。我的程序源代码如下：

#include<stdio.h>
#include<string.h>
bool nprime[101];
int a[40],i,j,ans,val[10001];
int calc(int s)
{
int ret=1,t,i;
for (i=1;i<=a[0]&&s!=1;i++)
{
t=1;
while (s%a[i]==0)
{
s/=a[i];
t*=a[i];
}
ret*=(t*a[i]-1)/(a[i]-1);
}
if (s!=1) return ret*(s+1);
else return ret;
}
int main()
{
memset(nprime,false,sizeof(nprime));
a[0]=0;
for (i=2;i<=100;i++)
if (!nprime[i])
{
a[++a[0]]=i;
for (j=i*i;j<=100;j+=i)
nprime[j]=true;
}
ans=0;
memset(val,-1,sizeof(val));
for (i=2;i<=10000;i++)
if (val[i]==-1)
{
val[i]=calc(i)-i;
if (val[i]<=10000&&val[i]>i)
{
val[val[i]]=calc(val[i])-val[i];
if (val[val[i]]==i)
{
ans+=i;
ans+=val[i];
}
}
}
printf("%d\n",ans);
return 0;
}