Prject Euler - Daybreakcx's Blog - Keep Programming! With Algorithm! With Fun!

Project Euler——Problem 35

原题与答案：

Problem 35

17 January 2003

The number, 197, is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime.

There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97.

How many circular primes are there below one million?

Answer:55

 

分析与解答：

这个题目是求1000000以内所有循环本身都是素数的数的个数，比如197循环本身就有197,971和719三个。这个题目最早的时候想要优化一下，避免重复求解，即既然循环一圈都是素数，那么求过的就一起在最小的那个算掉，不用重复求解了。但是这样计算有一个问题，算出的结果都是56，错误就在于11这个数，11自循环后就是本身，这里重复累计了一次，后来用最为朴素的算法得出了55才发现错在哪里，朴素的算法就是一个个素数去枚举，然后累加和，程序非常简单，关键就在打素数表，具体的实现源程序代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. bool nprime[1000001];
  4. int i,j,a[80000],ans;
  5. int check(int s)
  6. {
  7.         int i,j,k,cnt=0;
  8.         for (i=1,j=10;s>=j;i++,j*=10);
  9.         for (j/=10,k=1;k<i;k++)
  10.         {
  11.                 s=(s%j)*10+s/j;
  12.                 if (!nprime[s])
  13.                         cnt++;
  14.         }
  15.         return cnt==i-1;
  16. }
  17. int main()
  18. {
  19.         a[0]=0;
  20.         memset(nprime,false,sizeof(nprime));
  21.         for (i=2;i<=1000000;i++)
  22.                 if (!nprime[i])
  23.                 {
  24.                         a[++a[0]]=i;
  25.                         if (i<=1000)
  26.                                 for (j=i*i;j<=1000000;j+=i)
  27.                                         nprime[j]=true;
  28.                 }
  29.         ans=0;
  30.         for (i=1;i<=a[0];i++)
  31.                 if (check(a[i]))
  32.                         ans++;
  33.         printf("%d\n",ans);
  34.         return 0;
  35. }

 

 

Prject Euler Comments(0) 2009年8月17日 00:07

Project Euler——Problem 34

原题与答案：

Problem 34

03 January 2003

145 is a curious number, as 1! + 4! + 5! = 1 + 24 + 120 = 145.

Find the sum of all numbers which are equal to the sum of the factorial of their digits.

Note: as 1! = 1 and 2! = 2 are not sums they are not included.

Answer:40730

 

分析与解答：

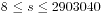这个题目是求除了1和2以外的等于自身各位数值阶乘的和的数，输出他们的和。题目本身的难点在于求范围，因为如果我们需要枚举的数值范围很大的话就要考虑用构造的方法了，所以我们先来判定一下一个n位数他的求值范围是n \leq s \leq n*9!，那么我们可以很容易想到那个n位数不可能是无限大的，因为每加上一位，和最大只添加9!=362880，于是通过尝试发现n为8的时候，求值范围是8 \leq s \leq 2903040，在最大值只有7位数，明显8位数不在我们的枚举范围之内。同时n为7的时候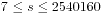7 \leq s \leq 2540160，还可能存在所求的数值，因此我们枚举的范围最后定下来是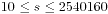10 \leq s \leq 2540160，自然就得到了如下程序源代码了：

 

  1. #include<stdio.h>
  2. int fact[10],base[10],i,j,s,ans;
  3. int calc(int s)
  4. {
  5.         int ret=0;
  6.         while (s)
  7.         {
  8.                 ret+=fact[s%10];
  9.                 s/=10;
  10.         }
  11.         return ret;
  12. }
  13. int main()
  14. {
  15.         fact[0]=1;
  16.         for (i=1;i<=9;i++) fact[i]=fact[i-1]*i;
  17.         base[0]=1;
  18.         for (i=1;i<=7;i++) base[i]=base[i-1]*10;
  19.         for (s=fact[9],i=2;i<=7;i++)
  20.         {
  21.                 s+=fact[9];
  22.                 for (j=base[i-1];j<base[i]&&j<=s;j++)
  23.                         if (calc(j)==j) ans+=j;
  24.         }
  25.         printf("%d\n",ans);
  26.         return 0;
  27. }

 

 

Prject Euler Comments(0) 2009年8月16日 23:29

Project Euler——Problem 33

原题与答案：

Problem 33

20 December 2002

The fraction ^(49)/_(98) is a curious fraction, as an inexperienced mathematician in attempting to simplify it may incorrectly believe that ^(49)/_(98) = ^(4)/_(8), which is correct, is obtained by cancelling the 9s.

We shall consider fractions like, ^(30)/_(50) = ^(3)/_(5), to be trivial examples.

There are exactly four non-trivial examples of this type of fraction, less than one in value, and containing two digits in the numerator and denominator.

If the product of these four fractions is given in its lowest common terms, find the value of the denominator.

Answer:100

 

分析与解答：

这个题目是说形如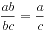\dfrac{ab}{bc}=\dfrac{a}{c}的小于1的分数一共有四个，其中ab和bc均为两位数，问这四个分数的乘积的最简分式的分母是什么。这个题目很明显是一个枚举题，这里要用到的就是一个最大公约数的过程，求最大公约数我们可以利用辗转相除法来实现，然后分别依次枚举b,a和c，要注意的是三个数都必须非0，而且c>a，实际上这题的实现很简单，具体的程序源代码如下所示：

  1. #include<stdio.h>
  2. int i,j,k,s,t,num,den;
  3. int gcd(int x,int y)
  4. {
  5.         int t;
  6.         while (t=x%y)
  7.         {
  8.                 x=y;
  9.                 y=t;
  10.         }
  11.         return y;
  12. }
  13. int main()
  14. {
  15.         num=den=1;
  16.         for (i=1;i<10;i++)
  17.                 for (j=1;j<10;j++)
  18.                         for (k=j+1;k<10;k++)
  19.                         {
  20.                                 s=gcd(j*10+i,i*10+k);
  21.                                 t=gcd(j,k);
  22.                                 if ((j*10+i)/s==j/t&&(i*10+k)/s==k/t)
  23.                                 {
  24.                                         num*=j;
  25.                                         den*=k;
  26.                                 }
  27.                         }
  28.         printf("%d\n",den/gcd(num,den));
  29.         return 0;
  30. }

 

 

 

Prject Euler Comments(0) 2009年8月16日 23:04

Project Euler——Problem 32

原题与答案：

Problem 32

06 December 2002

We shall say that an n-digit number is pandigital if it makes use of all the digits 1 to n exactly once; for example, the 5-digit number, 15234, is 1 through 5 pandigital.

The product 7254 is unusual, as the identity, 39 × 186 = 7254, containing multiplicand, multiplier, and product is 1 through 9 pandigital.

Find the sum of all products whose multiplicand/multiplier/product identity can be written as a 1 through 9 pandigital.

HINT: Some products can be obtained in more than one way so be sure to only include it once in your sum.

Answer:45228

 

分析与解答：

这个题目是求所有的满足条件的乘法表达式的积的和，题目中的条件是要求表达式中出现1到9这9个数字，每个有且只有一次。仔细分析一下去掉一些不可能的情况，首先是我们的表达式里面一共有9个数字，这样我们先考虑生成9的全排列，然后再加入乘号和等号，同时考虑到我们加入乘号和等号的情况总数为C(8,2)=28种，我们可以从这里排除掉一大堆不可能的情况。对于一个n位数和一个m位数的乘法，他们的积只可能是n+m或者是n+m-1位数，于是乎我们可以假设当被乘数小等于乘数的时候，我们得到的只可能有两种情况符合题意，即1位数*4位数=4位数或者是2位数*3位数=4位数，这样我们就将情况数从28种缩减到了2种，然后就是枚举计算的事情了，实际上满足条件的表达式非常少，因为积都是4位数，不会超过P(9,4)=3024个，但是实际算出来只有9个。我的程序源代码如下所示：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. #include<algorithm>
  4. int list[10],prod[3100],i,j,ans,s,t,u;
  5. bool yet[10],first=true;
  6. void check()
  7. {
  8.         int i;
  9.         for (u=0,i=5;i<9;i++) u=u*10+list[i];
  10.         for (s=i=0;i<1;i++) s=s*10+list[i];
  11.         for (t=0,i=1;i<5;i++) t=t*10+list[i];
  12.         if (s&&t>=1000&&u>=1000&&s*t==u)
  13.                 prod[++prod[0]]=u;
  14.         for (s=i=0;i<2;i++) s=s*10+list[i];
  15.         for (t=0,i=2;i<5;i++) t=t*10+list[i];
  16.         if (s>=10&&t>=100&&u>=1000&&s*t==u)
  17.                 prod[++prod[0]]=u;
  18. }
  19. void calc(int pos)
  20. {
  21.         if (pos==9) check();
  22.         else
  23.                 for (list[pos]=1;list[pos]<=9;list[pos]++)
  24.                         if (!yet[list[pos]])
  25.                         {
  26.                                 yet[list[pos]]=true;
  27.                                 calc(pos+1);
  28.                                 yet[list[pos]]=false;
  29.                         }
  30. }
  31. int main()
  32. {
  33.         prod[0]=0;
  34.         memset(yet,false,sizeof(yet));
  35.         calc(0);
  36.         std::sort(prod+1,prod+prod[0]+1);
  37.         for (ans=0,i=j=1;;i=j)
  38.         {
  39.                 ans+=prod[i];
  40.                 while (j<=prod[0]&&prod[i]==prod[j])
  41.                         j++;
  42.                 if (j>prod[0]) break;
  43.         }
  44.         printf("%d\n",ans);
  45.         return 0;
  46. }

 

 

 

 

Prject Euler Comments(0) 2009年8月15日 05:12

Project Euler——Problem 31

原题与答案

Problem 31

22 November 2002

In England the currency is made up of pound, £, and pence, p, and there are eight coins in general circulation:

1p, 2p, 5p, 10p, 20p, 50p, £1 (100p) and £2 (200p).

It is possible to make £2 in the following way:

1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p

How many different ways can £2 be made using any number of coins?

Answer:73682

 

分析与解答：

题目是说给定八种币值：1,2,5,10,20,50,100,200，问组成200一共有多少种可能。这是一个很经典的找钱问题，当然当钱币数量不多的时候可以搜索，直接枚举找到答案，但是有一种更好的方法，那就是利用动态规划来求解，首先我们得到动态规划方程：\begin{displaymath}F[i][j]=\sum_{a[k]\leq j}{F[i-1][j-a[k]]}\end{displaymath}。其中F[i][j]表示用前i种币值拼出j有多少种，那么就很容易可以理解那个方程了。当然我们注意到，新的F[i]总是依赖于F[i-1]的，因此我们可以从这个方面来考虑缩减空间消耗，可以利用滚动数组来实现，这样我们的空间消耗就是2*n了，同时我们看到由于对于j的值总是利用比j小的值求得，因此我们可以换一种思路，利用j求j后面的值，这样就又一次减少空间为一个一维数组了，初始化的时候我们设置得到0这个值有1种方法，具体的实现见程序源代码：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int coins[8]={1,2,5,10,20,50,100,200},cnt[201],i,j;
  4. int main()
  5. {
  6.         memset(cnt,0,sizeof(cnt));
  7.         cnt[0]=1;
  8.         for (i=0;i<8;i++)
  9.                 for (j=0;coins[i]+j<=200;j++)
  10.                         cnt[j+coins[i]]+=cnt[j];
  11.         printf("%d\n",cnt[200]);
  12.         return 0;
  13. }

 

 

Prject Euler Comments(0) 2009年8月13日 06:17

Project Euler——Problem 30

原题与答案：

Problem 30

08 November 2002

Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:

1634 = 1^(4) + 6^(4) + 3^(4) + 4^(4)
8208 = 8^(4) + 2^(4) + 0^(4) + 8^(4)
9474 = 9^(4) + 4^(4) + 7^(4) + 4^(4)

As 1 = 1^(4) is not a sum it is not included.

The sum of these numbers is 1634 + 8208 + 9474 = 19316.

Find the sum of all the numbers that can be written as the sum of fifth powers of their digits.

Answer:443839
 

分析与解答：

这个题目的意思是找出所有的等于自己各个位数五次方的和的数（除了1），输出他们的和。题目书写起来很简单，关键难点在于数值范围的判断，因为首先我们的直观想法：如果我们不停的加0，那么数值可以不断变大，但是五次方和不变，同时如果我们加上其他数值，可以调节两者大小关系，貌似这个枚举量是无穷的，但是仔细分析下来，我们得到结论是这个数最多就6位，下面先列出一个表格：

N 0 1 2 3 4 5 6 7 8 9
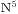N^5 0 1 32 243 1024 3125 7776 16807 32768 59049
0 1 0 -31 -242 -1023 -3124 -7775 -16806 -32767 -59048
1 10 9 -22 -233 -1014 -3115 -7766 -16797 -32758 -59039
2 100 99 68 -143 -924 -3025 -7676 -16707 -32668 -58949
3 1000 999 968 757 -24 -2125 -6776 -15807 -31768 -58049
4 10000 9999 9968 9757 8976 6875 2224 -6807 -22768 -49049
5 100000 99999 99968 99757 98976 96875 92224 83193 67232 40951
6 1000000 999999 999968 999757 998976 996875 992224 983193 967232 940951

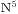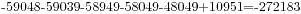首先上面的表格第二行表示N^5，然后下面每行都表示10^i-N^5，换句话说表示的是将数字j固定在i位会对原数减去本位的五次方造成多大的差值。我们的最终结果是在每行取且只取一列使得这些数值的和是0，那么我们如果要让原来数值尽量大，换句话说，如果我们要让数值的位数尽量多，我们就要取负值绝对值较大的，正值绝对值较小的。我们从表中得到我们从低位开始依次要取的数值是9，9，9，9，9，9，9，也就是说当取到6位的时候，不管怎么取，值都是正数，我们先把前5位取9，此时的数值是-59048-59039-58949-58049-48049+10951=-272183，这样就算我们最高位取值是0都会为正数，当然我们最高位不能取0，就取1吧，但不管怎么说，这个数值始终是保持在6位，不可能再大了，因此我们得到了范围后就可以放心枚举了，注意的一点是，最后的结果要把1去掉，我的程序源代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. #include<algorithm>
  4. int ft[10]={0,1,32,243,1024,3125,7776,16807,32768,59049},s,ans,a[6],b[6];
  5. bool get(int s)
  6. {
  7.         int i;
  8.         for (i=0;i<6;i++)
  9.         {
  10.                 b[i]=s%10;
  11.                 s/=10;
  12.         }
  13.         std::sort(b,b+6);
  14.         return !memcmp(a,b,sizeof(a));
  15. }
  16. int main()
  17. {
  18.         ans=0;
  19.         for (a[0]=0;a[0]<=9;a[0]++)
  20.                 for (a[1]=a[0];a[1]<=9;a[1]++)
  21.                         for (a[2]=a[1];a[2]<=9;a[2]++)
  22.                                 for (a[3]=a[2];a[3]<=9;a[3]++)
  23.                                         for (a[4]=a[3];a[4]<=9;a[4]++)
  24.                                                 for (a[5]=a[4];a[5]<=9;a[5]++)
  25.                                                 {
  26.                                                         s=ft[a[0]]+ft[a[1]]+ft[a[2]]+ft[a[3]]+ft[a[4]]+ft[a[5]];
  27.                                                         if (get(s)) ans+=s;
  28.                                                 }
  29.         printf("%d\n",ans-1);
  30.         return 0;
  31. }

 

 

Prject Euler Comments(0) 2009年7月27日 20:27

Project Euler——Problem 29

原题与答案：

Problem 29

25 October 2002

Consider all integer combinations of a^(b) for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:

2^(2)=4, 2^(3)=8, 2^(4)=16, 2^(5)=32
3^(2)=9, 3^(3)=27, 3^(4)=81, 3^(5)=243
4^(2)=16, 4^(3)=64, 4^(4)=256, 4^(5)=1024
5^(2)=25, 5^(3)=125, 5^(4)=625, 5^(5)=3125

If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:

4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125

How many distinct terms are in the sequence generated by a^(b) for 2 ≤ a ≤ 100 and 2 ≤ b ≤100?

Answer:9183

 

分析与解答：

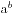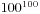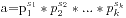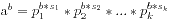题目的意思是由在[2,100]区间中的a和b由a^b形式构成的数有多少个。首先我们先确定一点，那就是a_1^{b_1}=a_2^{b_2}这样的情况是存在的，比如2^4=4^2，那么也就是说有重复的数值存在，其次是我们是否需要求出每一个数值的具体大小呢？答案是否定的，在[2,100]区间中，我们得到的最大数值是100^{100}，大概有201位，直接去算那么数值比较大，而且比较也很久，我们就要想换一种方法。我们利用一个更快的方法来进行，假设a的质因素分解形式是a=p_1^{s_1}*p_2^{s_2}*...*p_k^{s_k}，那么a^b=p_1^{b*s_1}*p_2^{b*s_2}*...*p_k^{b*s_k}，我们可以将所有的数值都化成质因素分解的形式，这样我们只需要比较对应的次数，而且在100内的素数只有25个，比较的个数比较少。每次我们分解出a的形式，然后对于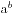a^b只要将次数都乘以b，就可以了，最后将这些次数序列排个序，计算有多少种即可，我的源程序代码如下所示：

 

  1. #include<stdio.h>
  2. #include<memory.h>
  3. #include<algorithm>
  4. bool nprime[101];
  5. int a[26],i,j,k,n,ans,temp[25];
  6. struct node
  7. {
  8.         int list[25];
  9. }res[9801];
  10. bool cmp(node s,node t)
  11. {
  12.         return memcmp(s.list,t.list,sizeof(res[0].list))<0;
  13. }
  14. void calc(int s)
  15. {
  16.         int i;
  17.         for (i=1;i<=a[0];i++)
  18.         {
  19.                 temp[i-1]=0;
  20.                 while (s%a[i]==0)
  21.                 {
  22.                         s/=a[i];
  23.                         temp[i-1]++;
  24.                 }
  25.         }
  26. }
  27. int main()
  28. {
  29.         a[0]=0;
  30.         memset(nprime,false,sizeof(nprime));
  31.         for (i=2;i<=100;i++)
  32.                 if (!nprime[i])
  33.                 {
  34.                         a[++a[0]]=i;
  35.                         if (i<=10)
  36.                                 for (j=i*i;j<=100;j+=i)
  37.                                         nprime[j]=true;
  38.                 }
  39.         n=0;
  40.         for (i=2;i<=100;i++)
  41.         {
  42.                 calc(i);
  43.                 for (j=2;j<=100;j++)
  44.                 {
  45.                         for (k=0;k<a[0];k++)
  46.                                 res[n].list[k]=temp[k]*j;
  47.                         n++;
  48.                 }
  49.         }
  50.         std::sort(res,res+n,cmp);
  51.         ans=0;
  52.         for (i=j=0;;)
  53.         {
  54.                 ans++;
  55.                 while (j<n&&!memcmp(res[i].list,res[j].list,sizeof(res[0].list))) j++;
  56.                 if (j==n) break;
  57.                 i=j;
  58.         }
  59.         printf("%d\n",ans);
  60.         return 0;
  61. }

 

 

Prject Euler Comments(0) 2009年7月27日 18:58

Project Euler——Problem 28

原题与答案：

Problem 28

11 October 2002

 

Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:

21 22 23 24 25
20  7  8  9 10
19  6  1  2 11
18  5  4  3 12
17 16 15 14 13

It can be verified that the sum of both diagonals is 101.

What is the sum of both diagonals in a 1001 by 1001 spiral formed in the same way?

Answer:669171001
 

分析与解答：

这题是求按照顺时针从中间展开的1001*1001的方阵对角线上数字的和，其实很简单，最初想法肯定是先列出这个方阵，然后求，但是实际上不用，我们一圈一圈来看，除了最里圈只有一个数字1外，其余都是四个数字，而且实际上沿着1向右上角走去是奇数的平方，那么我们可以根据[2*(k+1)-1]^2-(2*k-1)^2=(2*k+1)^2-(2*k-1)^2=8*k对角线上的最大数值的差是8乘以圈数-1，这样我们对于每一圈处理四个数值即可，最后便能很轻松得到结果，我的源程序代码如下所示：

 

  1. #include<stdio.h>
  2. int i,j,ans;
  3. int main()
  4. {
  5.         ans=1;
  6.         for (i=1,j=2;i<1002001;i+=4*j,j+=2) ans+=i*4+j*10;
  7.         printf("%d\n",ans);
  8.         return 0;
  9. }

 

 

Prject Euler Comments(1) 2009年7月27日 17:58

Project Euler——Problem 27

原题与答案：

Problem 27

27 September 2002

 

Euler published the remarkable quadratic formula:

n² + n + 41

It turns out that the formula will produce 40 primes for the consecutive values n = 0 to 39. However, when n = 40, 40^(2) + 40 + 41 = 40(40 + 1) + 41 is divisible by 41, and certainly when n = 41, 41² + 41 + 41 is clearly divisible by 41.

Using computers, the incredible formula  n² - 79n + 1601 was discovered, which produces 80 primes for the consecutive values n = 0 to 79. The product of the coefficients, -79 and 1601, is -126479.

Considering quadratics of the form:

n² + an + b, where |a| < 1000 and |b| < 1000

where |n| is the modulus/absolute value of n
e.g. |11| = 11 and |-4| = 4

Find the product of the coefficients, a and b, for the quadratic expression that produces the maximum number of primes for consecutive values of n, starting with n = 0.

 

Answer:-59231
 

分析与解答：

题目是求两个系数a和b，使得他们构成式子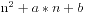n^2+a*n+b，然后将n从0开始取值，直到不是素数为止，现在我们要在a和b的绝对值都在1000内的范围中找出能够令n取到最大的a和b，输出他们的乘积。本身这个题目不难，重点在于枚举和素数的判定，我们列一个素数表即可，考虑到题目中的提示，79的n已经是比较大的了，我们根据这个范围大概列了90000以内的素数表，然后穷举a和b，整个过程十分简单，我的源程序代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int ansa,ansb,ansn,a,b,n,i,j;
  4. bool nprime[90001];
  5. int calc(int a,int b)
  6. {
  7.         int i,s;
  8.         for (i=0;;i++)
  9.         {
  10.                 s=i*i+i*a+b;
  11.                 if (s<2||nprime[s]) break;
  12.         }
  13.         return i-1;
  14. }
  15. int main()
  16. {
  17.         memset(nprime,false,sizeof(nprime));
  18.         for (i=2;i<=300;i++)
  19.                 if (!nprime[i])
  20.                         for (j=i*i;j<=90000;j+=i)
  21.                                 nprime[j]=true;
  22.         ansn=-1;
  23.         for (a=-999;a<=999;a++)
  24.                 for (b=-999;b<=999;b++)
  25.                 {
  26.                         n=calc(a,b);
  27.                         if (n>ansn)
  28.                         {
  29.                                 ansa=a;
  30.                                 ansb=b;
  31.                                 ansn=n;
  32.                         }
  33.                 }
  34.         printf("%d\n",ansa*ansb);
  35.         return 0;
  36. }

 

 

 

Prject Euler Comments(2) 2009年7月27日 17:29

Project Euler——Problem 26

原题与答案：

Problem 26

13 September 2002

A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:

^(1)/_(2) =  0.5
^(1)/_(3) =  0.(3)
^(1)/_(4) =  0.25
^(1)/_(5) =  0.2
^(1)/_(6) =  0.1(6)
^(1)/_(7) =  0.(142857)
^(1)/_(8) =  0.125
^(1)/_(9) =  0.(1)
^(1)/_(10) =  0.1

Where 0.1(6) means 0.166666..., and has a 1-digit recurring cycle. It can be seen that ^(1)/_(7) has a 6-digit recurring cycle.

Find the value of d < 1000 for which ^(1)/_(d) contains the longest recurring cycle in its decimal fraction part.

Answer:983

 

分析与解答：

这个题目是求在1000内的某个整数，其循环节最长。这个题目其实是很简单的，先说说常规算法，常规的方法直接想到的是列出各个位数，然后强行判定循环节，这样算法的复杂度十分的高，等待必然也是很漫长的。我们可以换个角度考虑，利用数学知识来想问题，从除法的运算法则入手，我们做除法无非就是每次将上次的余数乘以10然后再对除数取余，如此往复，那么循环节有什么特点呢？当前的余数相同！相同的余数必然引出一个相同的商序列，也就是我们的结果数字排列，因此我们的算法就非常简单了，先利用一个数值表示每次的余数，一直取余直到其重复出现为止，此时两次出现的距离就是我们的循环节了。那么我们需要最多判断多少次呢？根据取余规则我们可以肯定是不超过除数自身的非负整数，因此规模实际上十分的小，这题可以很轻松的解决，下面是我的程序源代码：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int i,ans,best,t,fir[1000];
  4. int calc(int s)
  5. {
  6.         int i,mod=1;
  7.         memset(fir,-1,sizeof(fir));
  8.         for (i=0;;i++)
  9.         {
  10.                 mod=(mod*10)%s;
  11.                 if (fir[mod]==-1) fir[mod]=i;
  12.                 else return i-fir[mod];
  13.         }
  14. }
  15. int main()
  16. {
  17.         ans=0;
  18.         best=0;
  19.         for (i=1;i<1000;i++)
  20.         {
  21.                 t=calc(i);
  22.                 if (t>best)
  23.                 {
  24.                         best=t;
  25.                         ans=i;
  26.                 }
  27.         }
  28.         printf("%d\n",ans);
  29.         return 0;
  30. }

 

 

Prject Euler Comments(0) 2009年7月27日 16:43