Project Euler——Problem 24

daybreakcx posted @ 2009年7月25日 08:06 in Prject Euler , 1094 阅读

原题与答案：

Problem 24

16 August 2002

A permutation is an ordered arrangement of objects. For example, 3124 is one possible permutation of the digits 1, 2, 3 and 4. If all of the permutations are listed numerically or alphabetically, we call it lexicographic order. The lexicographic permutations of 0, 1 and 2 are:

012 021 102 120 201 210

What is the millionth lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9?

Answer:2783915460

分析与解答：

这个题目是求10个数（0到9）的第1000000个字典序排列是多少，本身由于10!=3628800，完全在我们的承受范围之内，所以你可以直接枚举，但是这样做的复杂度是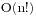 O(n!) ，在个数比较多的时候就是一场噩梦，我们利用一种复杂度是 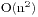O(n^2) 的算法来完成这题。首先我们来分析一下，当前面的某些位数确定后，其实以他们为前缀的排列是令他们固定，然后将剩下的数值进行全排列，也就是说对于一个第k大的排列，我们从左到右确定某个位的数值时候只要判定对于这个数值位右边的全排列。假设右边有s位，那么固定第s+1位的数值就有s!种排列，于是乎我们等于是在找未使用过的第 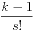$\dfrac{k-1}{s!}$ 大数值（之所以是k-1是要防止他被s!整除，使得后面出现第0大的数的情况），于是便有了如下的程序源代码：

#include<stdio.h>
#include<string.h>
bool yet[10];
int i,j,s,fac[10];
int main()
{
fac[0]=1;
for (i=1;i<=9;i++)
fac[i]=fac[i-1]*i;
memset(yet,false,sizeof(yet));
s=1000000;
for (i=9;i>=0;i--)
for (j=0;;)
if (yet[j]) j++;
else
if (s>fac[i])
{
s-=fac[i];
j++;
}
else
{
printf("%d",j);
yet[j]=true;
break;
}
printf("\n");
return 0;
}