二进制状态转移的最小覆盖问题

daybreakcx posted @ 2010年1月12日 21:11 in 算法 , 1838 阅读

前段时间参加了一场比赛，有个题目令我印象深刻，但是当时太忙，没时间记录下来，最近比较有空就暂做记录。

问题来自USACO CONTEST Elite 2009 November Competition这场比赛的golden组的名为lights的题目。

问题描述：

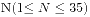$N(1\le N \le 35)$ 盏神器的灯之间有相互关联，初始状态下每盏灯都是熄灭状态，我们获得这些灯之间的关系的 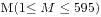$M(1\le M \le 595)$ 条边（无向且不重复），他们构成了一个无向图，当我们转换某盏灯的状态时候，与其有无向边相连的灯也全部转换状态（由点亮到熄灭或者由熄灭到点亮，而且包括执行转换的灯本身），给定这个无向图，并且告诉我们肯定存在操作令所有灯都点亮，问最少的转换执行次数是多少。

输入输出：

文件输入，输入文件为"lights.in"，包括两部分，第一部分位一行单独的两个整数N和M如描述中所示。第二部分包括M行，每行有两个数字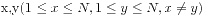 $x,y(1 \le x \le N,1 \le y \le N,x \ne y)$ 表示存在无向边的两个节点的编号。

文件输出，输出文件为"lights.out"，只要包括一个整数表示最少的转换执行次数就可以了。

样例输入输出：

输入：

输出：

输入输出说明：

共5个节点，六条边，其中我们分别对于1,4,5这三个节点进行转换操作，1转换后亮的灯为1,2,3；4转换后为1,4；5转换后为1,2,3,4,5。

问题分析：

我们先把问题转换一下，首先考虑怎么表示灯的状态，由于灯只有点亮和熄灭两种状态，而且灯的种数只有35,我们很自然地想到用一个二进制数来表示，其中每个位对应一个灯，0表示熄灭状态，1表示点亮，35位二进制数就够表示所有状态了。接下来是转换问题，进行一次转换可以看成某些位由0变成1,由1变成0，即对应位取反就可以了，我们很自然地想到某个一位二进制数异或上1即表示本身取反（直接原数取反无法满足要求，因为某些不受影响的灯也被转换了），我们读入数据的时候只要把有关联的灯都置1就可以了，一旦用这个灯，把这个转换值和当前状态异或就是下个状态。

使用的存储方式确定了，接下来是一些细节的考虑，一个灯会不会被执行转换两次以上呢？不可能！因为一个灯执行偶数次转换操作，等价于不执行操作，奇数次等价于执行一次，因此我们最后的实现全部灯都点亮的步骤只需要知道那些灯执行了一次转换操作就可以了。

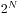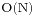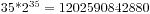按照上面的说法，我们有一个很自然的想法，就是枚举哪些灯进行过转换，也就是 2^N 个状态的枚举,每个状态用 O(N) 的时间进行判断，总体的时间复杂度是 $O(N*2^{N})$ 再回头看看N的范围，35！ $35*2^{35}=1202590842880$ ,不用想，一秒内肯定无法出结果。

既然无法直接枚举，我们就要想办法来间接减少枚举量。我们考虑将灯分为两组，前半组为前N/2个元素，记录为A，后半组为后N-N/2个元素，记录为B。我们如果单纯只枚举A或者B的话，时间上必然是够的。假设我们对于A进行枚举，获得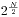 $2^{\frac{N}{2}}$ 个转换状态S，比如例子中5盏灯我们取灯1和2作为A，那么就有4个状态，都不取是0,只取灯1是(111)B=7，只取灯2是(11011)B=27，同时取灯1和2是7和25的异或是(11100)B=28,所以S就有四个元素{0,7,27,28},我们将这个集合反转，不考虑状态怎么来的，而只考虑用了多少灯，那么状态就可以变为一个二元组序列了{(0:0),(7:1),(27:1),(28:2)}，其中(x:y)表示获得状态x用了y盏灯，我们将这个序列排序，然后留作以后使用。接下来的工作是将A和B联系起来。

我们有了A的状态，同样可以有B的状态，样例中B有三个元素：3，4和5,得到它的S集合{(0:0),(29:1),(14:1),(22:1),(19:2),(11:2),(24:2),(5:3)}，我们需要做的工作就是在A的S和B的S中找两个数元素，使得他们的第一维的异或是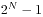 2^N-1 ，并且第二维的和最小，很显然A的S中(7:1)和B的S中(24:2)满足我们的要求，7^24=31，而其和为3最小，就是我们的答案。

于是我们的算法便有了，先求A的S，然后排序，然后求B的S，求出每项后在A的S中找可以搭配的项目，这里由于我们原先排序过，可以利用二分查找来实现，因此我们只需要存储下A的S集合，并且查找即可，时间复杂度是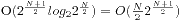 $O(2^{\frac{N+1}{2}}log_2{2^{\frac{N}{2}}})=O(\frac{N}{2}2^{\frac{N+1}{2}})$ ，空间复杂度为 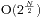$O(2^{\frac{N}{2}})$ ，均符合我们的要求，此题得解。

实现代码：

如下是我的实现代码，仅供参考：

#include<stdio.h>
#include<string.h>
#include<algorithm>
struct node
{
	int make;
	int cnt;
}list[131072];
int n,m,x,y,i,j,res,va,cn,pos,side[35];
bool cmp(node s,node t)
{
	if (s.make!=t.make) return s.make<t.make;
	else return s.cnt>t.cnt;
}
int find(int s)
{
	int f=0,t=(1<<(n>>1))-1,mid;
	while (f<t)
	{
		mid=f+((t-f+1)>>1);
		if (list[mid].make>s) t=mid-1;
		else f=mid;
	}
	if (list[f].make!=s) return -1;
	else return f;
}
int main()
{
	freopen("lights.in","r",stdin);
	freopen("lights.out","w",stdout);
	scanf("%d%d",&n,&m);
	for (i=0;i<n;i++) side[i]=(long long)1<<i;
	for (i=0;i<m;i++)
	{
		scanf("%d%d",&x,&y);
		side[x-1]|=(long long)1<<(y-1);
		side[y-1]|=(long long)1<<(x-1);
	}
	memset(list,0,sizeof(list));
	for (i=0;i<(1<<(n>>1));i++)
		for (j=0;j<(n>>1);j++)
			if (i&(1<<j))
			{
				list[i].make^=side[j];
				list[i].cnt++;
			}
	std::sort(list,list+(1<<(n>>1)),cmp);
	res=-1;
	for (i=0;i<(1<<(n-(n>>1)));i++)
	{
		va=cn=0;
		for (j=0;j<n-(n>>1);j++)
			if (i&(1<<j))
			{
				va^=side[j+(n>>1)];
				cn++;
			}
		va=((long long)1<<n)-1-va;
		pos=find(va);
		if (pos!=-1&&(res==-1||list[pos].cnt+cn<res))
			res=list[pos].cnt+cn;
	}
	printf("%d\n",res);
	return 0;
}