重温K&R(3)
最近要看的书好多，忙碌并快乐着，但是只要不乱了方寸就好，接着继续K&R的学习，这里是第三章，是关于流程控制的，我们可以用if-else啊，switch啊还有一些循环语句来实现，闲话少说，先把习题做上。
Exercise 3-1. Our binary search makes two tests inside the loop, when one would suffice (at the price of more tests outside.) Write a version with only one test inside the loop and measure the difference in runtime.
解：这里要说一下题目表达的是我们平时某些二分查找需要两个判断（if-else if-else），题目需要我们只用一个判断就实现，实际上这个很简单，用原先我关于二进制的专题里头的代码就是答案了，关键是原先判断的时候包含了一旦找到就直接退出的过程，我们可以将其省去，那么我们的程序就出来了。
int BinarySearch(int f, int t, int* a, int s)
{
int mid;
while (f < t)
{
mid = f + ((t - f) >> 1);
if (a[mid] >= s)
t = mid;
else
f = mid + 1;
}
if (a[f] == s)
return -1;
else
return f;
}
Exercise 3-2. Write a function escape(s,t) that converts characters like newline and tab into visible escape sequences like \n and \t as it copies the string t to s. Use a switch. Write a function for the other direction as well, converting escape sequences into the real characters.
解：这里就让我们很开心啦，让我们用switch做escape操作，就是将将不可见的字符（如回车啊，制表符啊）换成可见形式（对应的为"\n"和"\t"）。源串是s，目标串是t。这里的要求是用switch。同时题目又说了，让我们做一个反向的转换。我的程序作为例子处理回车和制表符，返回的函数是back（简单好用我就直接上了
），请见谅。
#include <stdio.h>
#include<string.h>
void escape(char s[], char t[])
{
int i, j;
for (i = j = 0; s[i]; i++)
switch (s[i]) {
case '\t':
t[j++] = '\\';
t[j++] = 't';
break;
case '\n':
t[j++] = '\\';
t[j++] = 'n';
break;
default:
t[j++] = s[i];
}
t[j] = 0;
}
void back(char s[], char t[])
{
int i, j;
for (i = j = 0; s[i]; i++)
if (s[i] == '\\') {
switch (s[i + 1]) {
case 'n':
t[j++] = '\n';
break;
case 't':
t[j++] = '\t';
break;
default:
t[j++] = s[i + 1];
break;
}
i++;
}
else
t[j++] = s[i];
t[j] = 0;
}
int main()
{
char a[500] = "fkjewk jf le\tkjfk\ndf\nfds",b[500];
escape(a, b);
printf("a = %s\nb = %s\n", a, b);
strcpy(a, b);
back(a, b);
printf("a = %s\nb = %s\n", a, b);
return 0;
}
Exercise 3-3. Write a function expand(s1,s2) that expands shorthand notations like a-z in the string s1 into the equivalent complete list abc...xyz in s2. Allow for letters of either case and digits, and be prepared to handle cases like a-b-c and a-z0-9 and -a-z. Arrange that a leading or trailing - is taken literally.
解：这个题目要我们展开所有的可能的区间表达式，比如0-5展开成012345这样的，我的函数操作了大小写和数字的序列，上升下降的都有，左右区间相同的我并没有给以处理。
void expand(char s1[], char s2[])
{
int i, j, k, mov;
for (i = j = 0; s1[i]; i++)
if (s1[i] == '-' && i > 0 && s1[i - 1] != s1[i + 1] &&
((s1[i - 1] >= '0' && s1[i - 1]<= '9' && s1[i + 1] >= '0' && s1[i + 1] <= '9') ||
(s1[i - 1] >= 'a' && s1[i - 1]<= 'z' && s1[i + 1] >= 'a' && s1[i + 1] <= 'z') ||
(s1[i - 1] >= 'A' && s1[i - 1]<= 'Z' && s1[i + 1] >= 'A' && s1[i + 1] <= 'Z'))) {
if (s1[i + 1] > s1[i - 1])
mov = 1;
else
mov = -1;
for (k = s1[i - 1] + mov; k != s1[i + 1]; k += mov)
s2[j++] = k;
}
else
s2[j++]=s1[i];
s2[j] = 0;
}
Exercise 3-4. In a two's complement number representation, our version of itoa does not handle the largest negative number, that is, the value of n equal to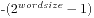 
. Explain why not. Modify it to print that value correctly, regardless of the machine on which it runs.
解：这里说当n在补码存储的条件下取值负最大的时候原函数无法表示，关键问题在于如果是负最大的话那么其补码表示为除了符号为是1其他都是0,而其相反数是无法用补码表示的（少了1），但是不管如何，我们只要稍微改改就可以让原来的程序继续使用，关键是如何对付负最大的情况，考虑到其实不管正负，如果我们保留原数进行计算，取余的时候加上绝对值那么就可以正常计算了，这就是主要的思想，我的程序也是如此的。
void itoa(int n, char s[])
{
int i, sign = n;
i = 0;
do {
s[i++] = abs(n % 10) + '0';
} while (n /= 10);
if (sign < 0)
s[i++] = '-';
s[i] = '\0';
reverse(s);
}
Exercise 3-5. Write the function itob(n,s,b) that converts the integer n into a base b character representation in the string s. In particular, itob(n,s,16) formats s as a hexadecimal integer in s
解：题目改来改去实际上没怎么变化，这里要我们重新写一个函数，它的作用是在原来的基础上加入进制的因素，也就是变成b进制表示，但是不管如何，只是我们在表示的时候对于大于10的数值进行A开始的替换，其他的只要将原来程序中具体数字10换成b就是我们要的程序了，非常之简单（PS：我只弄到62进制，再高我想不到可以用来表示的东西了）。
void itoa(int n, char s[], int b)
{
int i, t, sign = n;
i = 0;
do {
t = abs(n % b);
if (t <= 9)
s[i++] = t + '0';
else if (t <= 35)
s[i++] = t - 10 + 'A';
else
s[i++] = t - 36 + 'a';
} while (n /= b);
if (sign < 0)
s[i++] = '-';
s[i] = '\0';
reverse(s);
}
Exercise 3-6. Write a version of itoa that accepts three arguments instead of two. The third argument is a minimum field width; the converted number must be padded with blanks on the left if necessary to make it wide enough.
解：题目难度不如上一个，要求只有限制宽度，就是不够的时候用空格补齐就可以了，这个很容易办到，只要在3-4的基础上往后添加空格就行，代码改动不大。
void itoa(int n, char s[], int w)
{
int i, t, sign = n;
i = 0;
do {
s[i++] = abs(n % 10) + '0';
} while (n /= 10);
if (sign < 0)
s[i++] = '-';
for (; i < w; i++)
s[i] = ' ';
s[i] = '\0';
reverse(s);
}
小结：这一章题目不多，单纯认识知识的话内容相对简单，有些细节还是需要注意的。
1.关于switch最后的default，其break最好还是加上，特别是当你增减新功能的时候防止由于遗漏break而增加这个特殊的bug
2.正如原文所说do-while语句中do后的花括号最好还是加上，不然鬼知道你以后会不会再加东西进去
3.对于goto语句我不发表任何意见，用就用，用好就行
评论 (0)
