Introduction——1

如果是半年前，你问我啥是Machine Learning，我可以很肯定地跟你说：我不知道。现在呢？大概知道一点点，或许是我才开始意识到自己大概知道一点点，同时我还意识到这个学科很牛逼。

先说些闲话

最近是毕设季，实验室诸君都在积极准备，观察发现很多人在做手势识别（实验室做了好几届了，还在做，不发表评论，汗::>_<::），还有在做无人驾驶小车，然后根据目前他们的进程，大概问了一下，大都是神经网络之类的，加上半年的实习所接触的内容，我突然发现：我靠，大家都开始机器学习了！

半年前看Andrew Ng的Machine Learning视频（当初域名是ml-class.org，现在已经归到coursera里头了），当时大概了解了一下，classification、regression还有SVM神马的，但是都是一点皮毛，可还是发现这玩意儿太强大了，只要你有数据，你就能识别手写字体，你就能做无人驾驶车，可以让直升机自己学特技，总之各种可以。有这等好东西，自然要参合一下，略懂一下了，可惜半年前忙着优化，没好好学，不过现在我想自己大概有那时间了吧，所以抱起这本大部头细细学一下（大概七百页，偷偷告诉你网上有地方下彩色的，淘宝也能帮忙印，很方便）。

好了，闲话少叙，开始做第一章的笔记，给自己加了个油，一定坚持下来

第一个例子

第一张主要是介绍性的，首先作者举了个常见的例子：手写数字识别。

给定如下图的0～9的数字，要将他们识别出来，任务很明了：

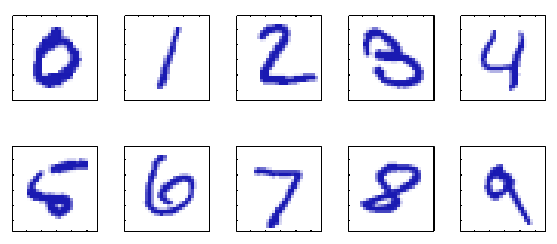
每个数字都是一个28*28像素的图像（表示时就是一个784个实数的向量），任务就是根据一个向量判断出这个数字是0～9中的哪一个。

常规情况下，或者说以前，我们会采用人工确定一些规则或启发式的方法来识别，这就需要对每个字进行很详细的分析，一不小心所需要的规则就会暴增，同时当然也会导致运行时间等暴增，而且最后得到的效果不是很好。

但是这个问题如果交给ML（Machine Learning）就轻松多了。由于它们对应数字我们已知，我们将这些数字视为这些图的类（category），每个图对应一个类，这样众多输入数据构成了我们的训练集（training set），并且利用它们来构建我们的模型（model）。我们将这些类放到一起形成了一个向量t，称为目标向量（target vector），此时图和其类之间就建立了对应关系了。

这时候，我们这个机器学习算法的执行目的就是：获取一个函数\(y(\vec{x})\)，其以新的数字图像\(\vec{x}\)为输入，输出它的类\(y(\vec{x})\)，而函数是在训练（或学习）的过程中确定的（我们的训练集用上了）。

这里涉及到一个称为generalization的词，据说是从心理学那边引过来的，大概就是说能这个正确识别新数据的能力，比如我们上面的例子，就是说你另一个人写的数字，传给这个函数，也能正确得到它是几，这是模式识别的主要目标。

一般来说，在做这些步骤之前，会先进行预处理（pre-processing），比如说我们把不同的特征的数值放缩到同一个数量级等，其目的是为了方便解决问题以及为模型加速，而上面的例子里，如果我们给每个数字限定一下其外框，让它们有固定的大小（28*28像素），这时候解决问题就更容易一点了，而既然我们对训练集进行了这个预处理，同样我们对测试集进行预处理也就是很必要的了。通过预处理，可以在速度上有所提升。同样，如果我们再进一步，比如你的图像再次减少特征数量，每次不是一个像素一个像素构成\(\vec{x}\)，减少计算量，使用这样一种方法：将小正方形内像素值平均值当成一个像素，我们取4*4的小方格，那么像素个数从原来的784变成了49个，这个过程常叫做特征提取（feature extraction），即从中提取有代表性的特性，但是同时有可能在数据上有所丢失，所以需要谨慎对待。

ML的分类

关于ML的概念不少，比如在对算法分类上就有好几种，比如我们根据输入数据的形式就能分出两种：监督学习（supervised learning）以及非监督学习（unsupervised learning）。前者就是我们例子里头呈现的，训练集里头包含了图像对应的类，也就是说同时包含输入向量和输出向量。而后者则少了输出向量那一部分，需要通过你的算法自行判定。举个例子我摆了一些苹果和香蕉在桌上，叫来一个小朋友，一个个告诉他哪个是苹果，哪个是香蕉，教会他识别，这个就叫做监督学习，而我如果不告诉他哪些是苹果，哪些是香蕉，让小朋友自己区分，这个就叫非监督学习。

监督学习常常有两种问题，一种叫做分类（classification），比如我们上面的识别手写数字，而另一种这是在类别是连续值的情况下的，称为回归（regression）。

对于非监督学习，常常有三种问题，一个叫做聚类（clustering），它将数据中相似度较高的归到一组中，此外还有密度估计（density estimation）问题，是用来估计输入数据空间的分布的，同时还有可视化（visualization）问题，目的是将数据从高维空间降至二维或者三维上。

当然除了上面说到的两种外，还有一种称为强化学习（reinforcement learning）的存在，这类问题是为了实现一种环境到行为的映射，同时使得这种行为让规定的收益评估最大化。一般其与监督学习进行比较，我们并未为其提供具体的分类等信息，而是针对在产生行为后，根据环境中的信息进行评估，判定行为的好坏，并且强化好的一方，在不断的学习过程中实现。其实际生活中就像是下棋一样，从一个新手一次次地与人博弈，学习自己每次输棋的原因，最后称为高手。

多项式曲线拟合（polynomial curve fitting）

书中给了一个多项式曲线拟合的例子，这是一个很常见的线性回归的例子，问题大概是说给定一个包含x（一条曲线）的N个观察结果（一些点坐标对）的训练集，记为向量\(\vec{x} \equiv (x_1,x_2, \cdots x_n)^T\)以及对应的向量\(\vec{t} \equiv (t_1, t_2, \cdots, t_n)^T\)（训练集构造在书中是以\(\sin(2\pi x)\)在[0,1]的范围内随机取10个点，然后对t添加一定的随机噪声产生的），我们的目的就是当有新的输入\(\widehat{x}\)的时候，能够得到相应的\(\widehat{t}\)，换句话说，实际上是要在某种程度上获取\(\sin(2\pi x)\)这个函数。

怎么做呢？我们用一个多项式去拟合这个三角函数，我们假设我们的多项式函数是：

\[y(x,\vec{\omega}) = \omega_0 + \omega_1 x + \omega_2 x^2 + \cdots + \omega_M x^M = \sum_{j=0}^{M}{\omega_j x^j}\]

其中M为其阶数（order），而向量\(\vec{\omega}\)是其系数向量，对于x来说，\(y(x,\vec{\omega})\)是一个非线性函数，但对向量\(\vec{\omega}\)来说，其是一个线性函数，而这个函数的未知变量是\(\vec{\omega}\)，则称这种模型为线性模型（linear models）。

怎么确定这个位置向量呢？或者换句话说，什么样的向量是最好的呢？如果我们有相应的指标，就能选出最好的那个向量，我们的模型就出来了，这里有一个简单的方法，是使用误差函数（error function），他的定义如下：

\[E(\vec{\omega}) = \frac{1}{2}\sum_{n=1}^{N}{\{y(x_n,\vec{\omega})-t_n\}^2}\]

此处1/2是为了后面方便计算（后面会求导），求出的值是求得的函数值与目标值\(t_n\)的差平方和（也就是垂直距离平方和），我们的目标就是要求\(\vec{\omega}\)使得函数E最小化（很容易理解，最好情况下是这个多项式函数穿过所有的测试集中点，这样E就为0了）。

当然，这是针对同样的N值，如果N不一样怎么办呢，可以转化一下么，用下面的公式：

\[E_{RMS} = \sqrt{\frac{2E(\vec{\omega})}{N}}\]

这里RMS是指均方根（root-mean-square），这样就可以把不同规模的N拉到同一个比较等级上了。

接下来就是M的选取问题了，M应该选多少呢？首先如果要保证一定穿过所有的点，\(M \ge N\)肯定是可以的，但是会产生如下情况：

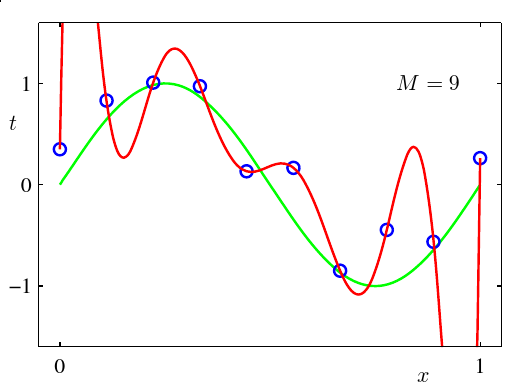
点是都串起来了，但是太曲折了吧（-_-!），这个现象叫做过度拟合（over-fitting），这种情况下好处是对于训练集能够很好地匹配，但是一旦引入测试集，点就有可能和曲线偏离非常大，实际上是一种应该避免的行为。

当然还有另一种极端，如下图所示：

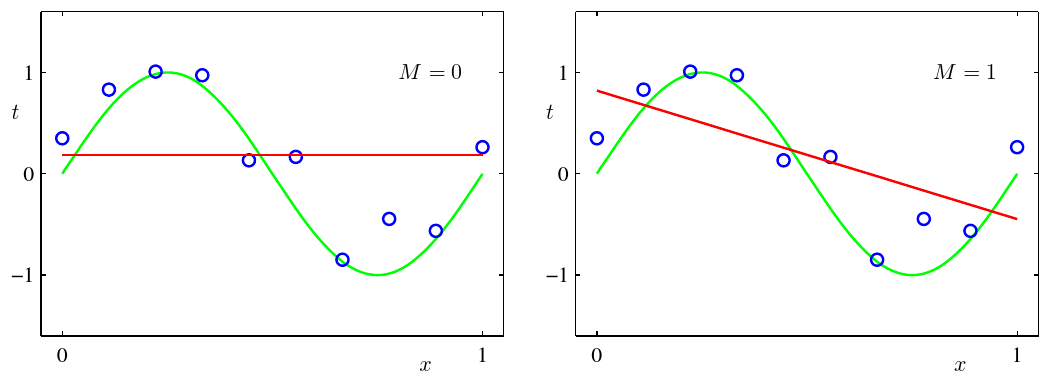
上图俩情况下M都太小了，串不下来什么点，这种情况叫做欠拟合（under-fitting），实际上效果也是很差的，甚至连训练集都没能很好地拟合，更何况是测试集了。所以选择一个较好的M值就显得很重要了，比如说我们这个例子里头选取不同的M得到的\(E_{RMS}\)比较图如下：

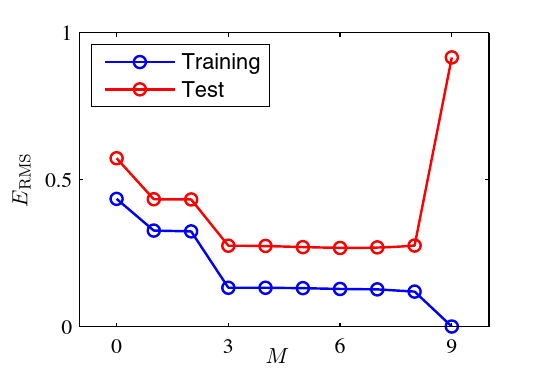
从3到8都能达到很好的效果，但是其他的就有点离谱了，要么是较小的M的时候在测试集和训练集都表现得不够好，要么就是9的时候测试集表现得离谱。

这还不是最离谱的，实际上离谱的是我们求出来的向量\(\vec{\omega}\)，我们来看看比较：

在M为9的时候，系数都大的离谱，这是因为为了去贴合那些点造成的（勉强没幸福么）。当然在训练集变大的时候，过度拟合问题就没那么明显了（这个很容易懂，完全过所有的点需要更高的多项式，而原来的次数就显得没那么大了，或许会慢慢向欠拟合演变）。

那我们是否有一种较好的处理方式呢？我们看看上面的系数，会有一个想法，如果那些系数没那么大会怎么样呢，一些高次的多项式，如果高次系数接近0，那么实际上就接近于降次了，所以限制系数是一个可行的方法，这个叫做规则化（regularization），是将误差函数改成如下形式：

\[\tilde{E}(\vec{\omega})=\frac{1}{2}\sum_{n=1}^{N}{\{y(x_n,\vec{\omega})-t_n\}^2}+\frac{\lambda}{2}{\left\|\vec{\omega}\right\|}^2\]

这里\({\left\|\vec{\omega}\right\|}^2\equiv\vec{\omega}^T\vec{\omega}=\omega_0^2+\omega_1^2+\omega_2^2+\cdots+\omega_M^2\)是向量的模的平方，而系数\(\lambda\)则表示这个部分的重要程度，如果\(\lambda\)较大，则对于系数的惩罚就越大，这样就使得系数的绝对值都会偏小，容易降次（无穷大的时候是极端情况，系数都为0的时候是最优值），产生欠拟合，而如果\(\lambda\)很小（比如0），则会消减系数的作用。这种减少系数值的方法称为shrinkage方法。

在机器学习中，若M为2，则称为ridge regression，而在神经网络里，这个方法叫做权值衰减（weight decay）。

加入这一项后效果如何呢？下图可以解释这一点：

\(\lambda\)为0，即\(\ln\lambda = -\infty\)时，这个方法被屏蔽了，不起作用，而当\(\lambda\)较小，即\(\ln\lambda = -18\)时，产生一定的效果，当\(\lambda\)较大 ，即\(\ln\lambda = 0\)时，就基本上让这条曲线变成了一条直线了。对于M为9的情况，下图描述了效果和\(\lambda\)之间的关系：

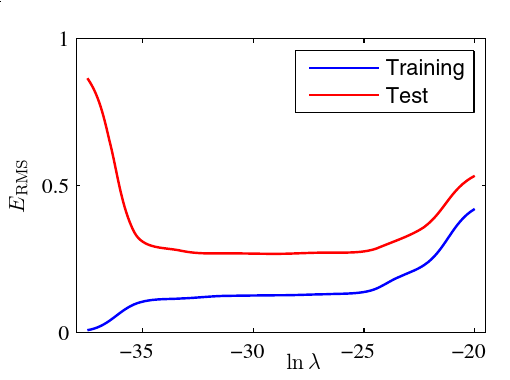
所以选择合适的\(\lambda\)也是很重要的（和M一起）。

好吧，第一篇先写这么多，后面继续，还是那句话，希望自己坚持到底