Project Euler——Problem 6 - Daybreakcx's Blog - Keep Programming! With Algorithm! With Fun!
Project Euler——Problem 6
daybreakcx
posted @ 2009年7月17日 20:57
in Prject Euler
, 1252 阅读
原题与答案:
Problem 6
14 December 2001
The sum of the squares of the first ten natural numbers is,
12 + 22 + ... + 102 = 385
The square of the sum of the first ten natural numbers is,
(1 + 2 + ... + 10)2 = 552 = 3025
Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is 3025 - 385 = 2640.
Find the difference between the sum of the squares of the first one hundred natural numbers and the square of the sum.
Answer:25164150
分析与解答:
这个题目是求1到100的和平方与平方和的差,我们可以很容易地利用求出通项公式。首先是和平方:![(1+2+...+n)^2=[\dfrac{n*(n+1)}{2}]^2=\dfrac{n^2*(n+1)^2}{4} (1+2+...+n)^2=[\dfrac{n*(n+1)}{2}]^2=\dfrac{n^2*(n+1)^2}{4}](/user_files/daybreakcx/epics/f9476d9e6356ce0e3bf90e895049ea2e8728ae3f.png) ,然后是平方和:
,然后是平方和: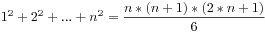 ,最后是他们的差:
,最后是他们的差: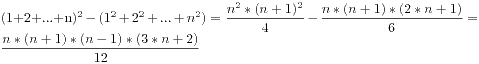 。于是带入公式就可以得到结果,当然用程序这个题目也是很容易实现的,源代码如下所示:
。于是带入公式就可以得到结果,当然用程序这个题目也是很容易实现的,源代码如下所示:
-
#include<stdio.h>
-
int res=0,i;
-
int main()
-
{
-
for (i=1;i<=100;i++)
-
res+=i;
-
res*=res;
-
for (i=1;i<=100;i++)
-
res-=i*i;
-
return 0;
-
}
2010年7月20日 03:41
菜鸟问一句:第二个平方和的公式是怎么推导出来的?请问是哪方面的数学知识……
2010年7月24日 03:43
实际上n次的连续自然数平方和是一个n+1次的多项式,这是我在初中时不知道听谁说的,后来也老这么用了,至于推导,网络上有很多,可以搜索一下
2010年7月24日 17:55
第二个分式的分母应该是6,你好像写错了。
2011年1月27日 03:31
多谢指正,已改过^_^