Project Euler——Problem 12

daybreakcx posted @ 2009年7月18日 22:17 in Prject Euler , 1124 阅读

原题与答案：

Problem 12

08 March 2002

The sequence of triangle numbers is generated by adding the natural numbers. So the 7^th triangle number would be 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. The first ten terms would be:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

Let us list the factors of the first seven triangle numbers:

1: 1
3: 1,3
6: 1,2,3,6
10: 1,2,5,10
15: 1,3,5,15
21: 1,3,7,21
28: 1,2,4,7,14,28

We can see that 28 is the first triangle number to have over five divisors.

What is the value of the first triangle number to have over five hundred divisors?

Answer:76576500

分析与解答：

这个题目本身不难，题意是求第一个约数个数超过500的“三角数”（第n个“三角数”是自然数1到n的和）。这个题目的难点在于求一个整数的约数个数，我们可以利用质因数分解的方法来进行统计，假设一个数的质因素分解为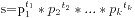 $s={p_1}^{t_1}*{p_2}^{t_2}*...*{p_k}^{t_k}$ ，那么他的约数个数是根据每个质因子的次数来决定的，即我们要的质因数个数是 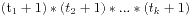(t_1+1)*(t_2+1)*...*(t_k+1) ，这个很容易理解，每个约数对应的质因数次数不会超过原数，同时也是每个质因数的次数的组合，可能的情况从0到最大的次数可取，然后利用乘法原理即我们的结果。因此本题只要利用质数的试除即可，我的素数表只开到10000，这样就可以对于100000000内的数进行质因数分解，初步估计答案是够的，实际上是正好比答案大一点。因此可以得到如下程序源代码：

#include<stdio.h>
#include<string.h>
bool nprime[10001];
int a[1300],i,j;
int calc(int s)
{
int i,t,ret=1;
for (i=1;i<=a[0]&&s!=1;i++)
{
t=0;
while (s%a[i]==0)
{
t++;
s/=a[i];
}
ret*=t+1;
}
if (s!=1) ret*=2;
return ret;
}
int main()
{
memset(nprime,false,sizeof(nprime));
a[0]=0;
for (i=2;i<=10000;i++)
if (!nprime[i])
{
a[++a[0]]=i;
if (i<=100)
for (j=i*i;j<=10000;j+=i)
nprime[j]=true;
}
for (i=1,j=0;;i++)
{
j+=i;
if (calc(j)>=500) break;
}
printf("%d\n",j);
return 0;
}