Project Euler——Problem 5
原题与答案:
Problem 5
2520 is the smallest number that can be divided by each of the numbers from 1 to 10 without any remainder.
What is the smallest number that is evenly divisible by all of the numbers from 1 to 20?
Answer:232792560
分析与解答:
本题求可以被1到20整除的最小的数是多少,这个根据数论性质可以很容易得出,我是笔算得到的结果,题目可以转化为求1到20的最小公倍数,这个问题有一种求法是利用求最大公约数得到:两个数的最小公倍数等于他们的乘积除以他们的最大公约数,而最大公约数可以利用辗转相除法轻松得到,但是这样对于像20这样的小数值未免有点浪费,于是可以用另一个知识:假设a质因数分解是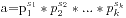 ,b的质因数分解是
,b的质因数分解是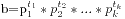 ,实际中两个数的质因数集合不一定相同,我们对于a有而b没有的质因数
,实际中两个数的质因数集合不一定相同,我们对于a有而b没有的质因数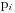 设置
设置 ,对于b有而a没有的质因数
,对于b有而a没有的质因数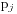 设置
设置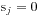 ,那么我们可以得到a和b的最小公倍数
,那么我们可以得到a和b的最小公倍数 ,利用这条性质我们只要求出每个小等于20的质数的可能得到的最大次数即可,具体实现见源代码:
,利用这条性质我们只要求出每个小等于20的质数的可能得到的最大次数即可,具体实现见源代码:
-
#include<stdio.h>
-
int plist[8]={2,3,5,7,11,13,17,19},s=20,ans=1,i,t;
-
int main()
-
{
-
for (i=0;i<8;i++)
-
{
-
t=1;
-
while (t<=s) t*=plist[i];
-
ans*=t/plist[i];
-
}
-
return 0;
-
}
Project Euler——Problem 4
原题与答案:
Problem 4
A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.
Find the largest palindrome made from the product of two 3-digit numbers.
Answer:906609
分析与解答:
这个题目也是很简单的,题目求两个三位数,使得他们的乘积是回文数,要求返回最大的满足条件的回文数,这里只需要枚举每对三位数,并且对他们的乘积进行判定输出最大值即可,编码没有什么难度,以下是实现代码:
-
#include<stdio.h>
-
int num[10],ans,i,j,s;
-
bool ispalindrome(int s)
-
{
-
int i,j;
-
num[0]=0;
-
while (s)
-
{
-
num[++num[0]]=s%10;
-
s/=10;
-
}
-
for (i=1,j=num[0];i<j;i++,j--)
-
if (num[i]!=num[j]) return false;
-
return true;
-
}
-
int main()
-
{
-
ans=0;
-
for (i=100;i<=999;i++)
-
for (j=i;j<=999;j++)
-
{
-
s=i*j;
-
if (s>ans&&ispalindrome(s)) ans=s;
-
}
-
return 0;
-
}
Project Euler——Problem 3
原题与答案:
Problem 3
The prime factors of 13195 are 5, 7, 13 and 29.
What is the largest prime factor of the number 600851475143 ?
Answer:6857
分析与解答:
题目的大意是求600851475143的最大质因子,这个问题的解决也很容易,只要将每个因子都试除从中取出最大的即可,但是要注意的是,如果单独去一个个试除的话,必然会导致运算的时间非常的久,我们考虑只需要计算到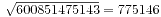 即可,因为如果有素因子大于这个数,那么通过对于小等于775146的素数的试除,剩下的数值一定是一个素数。所以我们可以一边利用筛法进行素数生成,一边进行试除将原来的数值变小,在C中这个题目的数值记录要用到64位整数,具体实现代码如下:
即可,因为如果有素因子大于这个数,那么通过对于小等于775146的素数的试除,剩下的数值一定是一个素数。所以我们可以一边利用筛法进行素数生成,一边进行试除将原来的数值变小,在C中这个题目的数值记录要用到64位整数,具体实现代码如下:
-
#include<stdio.h>
-
#include<string.h>
-
long long s,i,j,ans;
-
bool nprime[775147];
-
int main()
-
{
-
s=600851475143LL;
-
memset(nprime,false,sizeof(nprime));
-
for (i=2;i<=775146;i++)
-
if (!nprime[i])
-
{
-
if (s%i==0) ans=i;
-
while (s%i==0) s/=i;
-
if (s==1) break;
-
for (j=i*i;j<=775146;j+=i) nprime[j]=true;
-
}
-
if (s!=1) ans=s;
-
return 0;
-
}
Project Euler——Problem 2
原题与答案:
Problem 2
Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
Find the sum of all the even-valued terms in the sequence which do not exceed four million.
Answer:4613732
分析与解答:
这个题目也是简单的模拟,即求不超过4000000的偶数斐波那契数列项的和,笔算我没想到好方法,直接给出程序的运算方法吧:
-
#include<stdio.h>
-
int sum=2,a=1,b=2,i;
-
int main()
-
{
-
for (i=3;;i++)
-
if (i&1)
-
{
-
a+=b;
-
if (a>4000000) break;
-
if (!(a&1)) sum+=a;
-
}
-
else
-
{
-
b+=a;
-
if (b>4000000) break;
-
if (!(b&1)) sum+=b;
-
}
-
return 0;
-
}
Project Euler——Problem 1
原题与答案:
Problem 1
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below 1000.
Answer:233168
分析与解答:
这个题目描述很简单,是求小于1000的所有3或者5的倍数的和,第一个题就是a+b性质的,很容易过,刚开始我直接利用容斥原理笔算求出了结果。首先是小于1000的3倍数的和  ,接着是小于1000的5倍数的和
,接着是小于1000的5倍数的和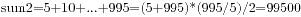 ,最后是小于1000的15的倍数
,最后是小于1000的15的倍数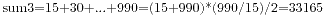 。于是我们要的结果
。于是我们要的结果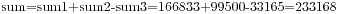 。
。
当然,这个题目用C写一下也不难,很容易就可以得到代码:
-
#include<stdio.h>
-
int i,sum;
-
int main()
-
{
-
sum=0;
-
for (i=1;i<1000;i++)
-
if (i%3==0||i%5==0) sum+=i;
-
return 0;
-
}
发现一个好玩的地方
临近领取毕业证书,闲来无事在网上闲逛,发现一个不错的地方,叫做Project Euler。这上面不要求提交代码,只要求给出答案,以数学题偏多,用了点时间把第一版的50题按照顺序给刷掉了,感觉很不错 。
。
原先有人给我提及过这个题库,当时没太在意,现在看看决定坚持做下去,数学题平时没事干可以练习一下思维,此外可以在上面练习高精度和数论等具体知识,准备在这上面写相应的解题报告,仅作记录 。
。
差点忘记说了,这个题库的地址是http://projecteuler.net/,注册一个帐号就可以做了,每过一题就可以得到一个勾,然后可以看到世界上其他人的解答,突然发现很多高人,有人用汇编A掉了不少题目,用python等的也不少,因为可以用来方便进行大数值计算,但我还是决定完全用C来进行解题 。
。