Prject Euler - Daybreakcx's Blog - Keep Programming! With Algorithm! With Fun!

Project Euler——Problem 25

原题与答案：

Problem 25

30 August 2002

The Fibonacci sequence is defined by the recurrence relation:

F_(n) = F_(n-1) + F_(n-2), where F_(1) = 1 and F_(2) = 1.

Hence the first 12 terms will be:

F_(1) = 1
F_(2) = 1
F_(3) = 2
F_(4) = 3
F_(5) = 5
F_(6) = 8
F_(7) = 13
F_(8) = 21
F_(9) = 34
F_(10) = 55
F_(11) = 89
F_(12) = 144

The 12th term, F_(12), is the first term to contain three digits.

What is the first term in the Fibonacci sequence to contain 1000 digits?

Answer:4782

 

分析与解答：

这个题目是求斐波那契数列的第几项开始是不小于1000位的，先整体估计一下，由于一个数s的位数为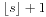\lfloor s \rfloor +1，那么根据斐波那契数列的通项公式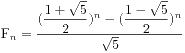F_n=\dfrac{({\dfrac{1+\sqrt{5}}{2}})^n-({\dfrac{1-\sqrt{5}}{2}})^n}{\sqrt{5}}，大概估计一下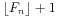\lfloor F_n \rfloor +1的范围，不是很大，在我们可以容忍的范围之内，于是我们可以利用高精度来进行计算，当然我们计算某一项的时候需要的值只有前两项，于是我们可以辗转迭代，最后就能获得结果，具体实现的源代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int f[2][2000],i,j,t,x;
  4. int main()
  5. {
  6.         memset(f,0,sizeof(f));
  7.         f[0][0]=f[0][1]=f[1][0]=f[1][1]=1;
  8.         for (i=3;;i++)
  9.         {
  10.                 t=0;
  11.                 x=1-(i&1);
  12.                 f[x][0]=f[1-x][0];
  13.                 for (j=1;j<=f[1-x][0];j++)
  14.                 {
  15.                         f[x][j]+=t+f[1-x][j];
  16.                         if (f[x][j]>=10)
  17.                         {
  18.                                 t=1;
  19.                                 f[x][j]-=10;
  20.                         }
  21.                         else t=0;
  22.                 }
  23.                 if (t) f[x][++f[x][0]]=1;
  24.                 if (f[x][0]>=1000) break;
  25.         }
  26.         printf("%d\n",i);
  27.         return 0;
  28. }

 

 

Prject Euler Comments(0) 2009年7月25日 08:39

Project Euler——Problem 24

原题与答案：

Problem 24

16 August 2002

A permutation is an ordered arrangement of objects. For example, 3124 is one possible permutation of the digits 1, 2, 3 and 4. If all of the permutations are listed numerically or alphabetically, we call it lexicographic order. The lexicographic permutations of 0, 1 and 2 are:

012   021   102   120   201   210

What is the millionth lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9?

Answer:2783915460

 

分析与解答：

这个题目是求10个数（0到9）的第1000000个字典序排列是多少，本身由于10!=3628800，完全在我们的承受范围之内，所以你可以直接枚举，但是这样做的复杂度是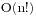O(n!)，在个数比较多的时候就是一场噩梦，我们利用一种复杂度是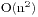O(n^2)的算法来完成这题。首先我们来分析一下，当前面的某些位数确定后，其实以他们为前缀的排列是令他们固定，然后将剩下的数值进行全排列，也就是说对于一个第k大的排列，我们从左到右确定某个位的数值时候只要判定对于这个数值位右边的全排列。假设右边有s位，那么固定第s+1位的数值就有s!种排列，于是乎我们等于是在找未使用过的第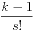\dfrac{k-1}{s!}大数值（之所以是k-1是要防止他被s!整除，使得后面出现第0大的数的情况），于是便有了如下的程序源代码：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. bool yet[10];
  4. int i,j,s,fac[10];
  5. int main()
  6. {
  7.         fac[0]=1;
  8.         for (i=1;i<=9;i++)
  9.                 fac[i]=fac[i-1]*i;
  10.         memset(yet,false,sizeof(yet));
  11.         s=1000000;
  12.         for (i=9;i>=0;i--)
  13.                 for (j=0;;)
  14.                         if (yet[j]) j++;
  15.                         else
  16.                                 if (s>fac[i])
  17.                                 {
  18.                                         s-=fac[i];
  19.                                         j++;
  20.                                 }
  21.                                 else
  22.                                 {
  23.                                         printf("%d",j);
  24.                                         yet[j]=true;
  25.                                         break;
  26.                                 }
  27.         printf("\n");
  28.         return 0;
  29. }

 

 

Prject Euler Comments(0) 2009年7月25日 08:06

Project Euler——Problem 23

原题与答案：

Problem 23

02 August 2002

A perfect number is a number for which the sum of its proper divisors is exactly equal to the number. For example, the sum of the proper divisors of 28 would be 1 + 2 + 4 + 7 + 14 = 28, which means that 28 is a perfect number.

A number n is called deficient if the sum of its proper divisors is less than n and it is called abundant if this sum exceeds n.

As 12 is the smallest abundant number, 1 + 2 + 3 + 4 + 6 = 16, the smallest number that can be written as the sum of two abundant numbers is 24. By mathematical analysis, it can be shown that all integers greater than 28123 can be written as the sum of two abundant numbers. However, this upper limit cannot be reduced any further by analysis even though it is known that the greatest number that cannot be expressed as the sum of two abundant numbers is less than this limit.

Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.

Answer:4179871

 

分析与解答：

题目中先定义了一种数，这种数的特点是他的所有小于本身的约数的和大于本身，然后阐述了一个结论，任何一个大于28123的整数都能写成两个这种数的和，要我们求不能写成两个这种数的和的数的总和。很自然地我们想到了一种解法，先枚举所有的那种数，然后获得所有小等于28123的两个这种数的和，最后把没出现的全部加起来就可以了。首先是这种数的枚举，由于12是最小的，所以枚举到28111即可，对于每个数判断小于他的约数的和是否大于本身。那么约数怎么求呢？在前面的文章中我们已经说过了，就是质因数分解，然后利用公式求得，这里就不再重复了，这样我们就能枚举出这些数了。最后我们要做的是求出所有是两个这种数的和的数。我们用一个bool数组表示一个数是否可以表示为两个这种数的和，然后我们利用二次时间把所有可以表示为两个这种数和的数标示，最后线型扫描一次就能完成任务了。我的程序员代码如下所示：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. bool nprime[168],can[28112];
  4. int a[50],s[7000],i,j,ans;
  5. int calc(int s)
  6. {
  7.         int i,ret=1,t;
  8.         for (i=1;s!=1&&i<=a[0];i++)
  9.         {
  10.                 t=1;
  11.                 while (s%a[i]==0)
  12.                 {
  13.                         s/=a[i];
  14.                         t*=a[i];
  15.                 }
  16.                 ret=ret*(t*a[i]-1)/(a[i]-1);
  17.         }
  18.         if (s!=1) return ret*(s+1);
  19.         else return ret;
  20. }
  21. int main()
  22. {
  23.         memset(nprime,false,sizeof(nprime));
  24.         a[0]=0;
  25.         for (i=2;i<=167;i++)
  26.                 if (!nprime[i])
  27.                 {
  28.                         a[++a[0]]=i;
  29.                         for (j=i*i;j<=167;j+=i)
  30.                                 nprime[j]=true;
  31.                 }
  32.         s[0]=0;
  33.         for (i=1;i<=28111;i++)
  34.                 if (calc(i)>(i<<1))
  35.                         s[++s[0]]=i;
  36.         memset(can,false,sizeof(can));
  37.         for (i=1;i<=s[0];i++)
  38.                 for (j=1;j<=s[0];j++)
  39.                         if (s[i]+s[j]>28111) break;
  40.                         else can[s[i]+s[j]]=true;
  41.         for (i=1;i<=28111;i++)
  42.                 if (!can[i]) ans+=i;
  43.         printf("%d\n",ans);
  44.         return 0;
  45. }

 

 

Prject Euler Comments(0) 2009年7月25日 06:08

Project Euler——Problem 22

原题与答案：

Problem 22

19 July 2002

Using names.txt (right click and 'Save Link/Target As...'), a 46K text file containing over five-thousand first names, begin by sorting it into alphabetical order. Then working out the alphabetical value for each name, multiply this value by its alphabetical position in the list to obtain a name score.

For example, when the list is sorted into alphabetical order, COLIN, which is worth 3 + 15 + 12 + 9 + 14 = 53, is the 938th name in the list. So, COLIN would obtain a score of 938 × 53 = 49714.

What is the total of all the name scores in the file?

Answer:871198282

 

分析与解答：

这个问题的题意是给定了一个大概64K的文本name.txt（这个文本的链接给出了，这里就不贴了，太废页面空间了），然后里面是一大堆人的名字，然后我们要做的操作是按照字典序排列后然后对每个名字单词求他的分数，分数的计算是每个字母在大写字母表中的排位的和，然后乘以他的序号，求这些分数的和。本身题目的描述把计算过程都给出了，估计这个题目也没有人会笔算吧（那就是神人了），我们就利用程序直接计算，这里只要注意读入的方式，然后排序计算就可以了，程序员源代码如下：

 

  1. #include<stdio.h>
  2. #include<algorithm>
  3. struct node
  4. {
  5.         char str[15];
  6. };
  7. node name[6000];
  8. int i,j,t,ans;
  9. bool cmp(node s,node t)
  10. {
  11.         return strcmp(s.str,t.str)<0;
  12. }
  13. int main()
  14. {
  15.         freopen("names.txt","r",stdin);
  16.         for (i=0;getchar()=='"';i++)
  17.         {
  18.                 for (j=0;(name[i].str[j]=getchar())!='"';j++);
  19.                 getchar();
  20.                 name[i].str[j]=0;
  21.         }
  22.         std::sort(name,name+i,cmp);
  23.         ans=0;
  24.         for (i=0;name[i].str[0];i++)
  25.         {
  26.                 t=0;
  27.                 for (j=0;name[i].str[j];j++)
  28.                         t+=name[i].str[j]-'A'+1;
  29.                 ans+=t*(i+1);
  30.         }
  31.         printf("%d\n",ans);
  32.         return 0;
  33. }

 

 

Prject Euler Comments(0) 2009年7月22日 05:50

Project Euler——Problem 21

原题与答案：

Problem 21

05 July 2002

Let d(n) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n).
If d(a) = b and d(b) = a, where a 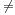\neq b, then a and b are an amicable pair and each of a and b are called amicable numbers.

For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.

Evaluate the sum of all the amicable numbers under 10000.

Answer:31626

 

分析与解答：

这个题目的意思是求10000内所有的相亲数的和，所谓的相亲数是指对于一对自然数，如果他们的小于本身的约数的和（不包括本身）等于对方的话，他们称为一对相亲数。这个题目可以通过枚举获得，其实实际上相亲数的数量非常少，首次做这个题的时候我是通过直接到网上查找获得的结果，而如果要写程序实现的话只要枚举10000以内的数值就可以一对对判断了。求所有约数的和可以先将原来的数值分解成如下形式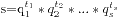：s=q_1^{t_1}*q_2^{t_2}*...*q_s^{t_s}，实际上获得所有约数的和就是将所有的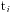t_i从0开始到本身进行枚举，然后将所有的枚举情况都加起来。假设其他的指数都不变的情况下，那么就相当于将其他确定的因数构成的元素看成一体当作公约数提取，本身这项就是形成了一个等比数列，因此我们要求的所有约数的和就是\dfrac{q_1^{t_1+1}-1}{q_1-1}*\dfrac{q_2^{t_2+1}-1}{q_2-1}*...*\dfrac{q_s^{t_s+1}-1}{q_s-1}，最后减去本身就是所有小于本身的约数的和了。我的程序源代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. bool nprime[101];
  4. int a[40],i,j,ans,val[10001];
  5. int calc(int s)
  6. {
  7.         int ret=1,t,i;
  8.         for (i=1;i<=a[0]&&s!=1;i++)
  9.         {
  10.                 t=1;
  11.                 while (s%a[i]==0)
  12.                 {
  13.                         s/=a[i];
  14.                         t*=a[i];
  15.                 }
  16.                 ret*=(t*a[i]-1)/(a[i]-1);
  17.         }
  18.         if (s!=1) return ret*(s+1);
  19.         else return ret;
  20. }
  21. int main()
  22. {
  23.         memset(nprime,false,sizeof(nprime));
  24.         a[0]=0;
  25.         for (i=2;i<=100;i++)
  26.                 if (!nprime[i])
  27.                 {
  28.                         a[++a[0]]=i;
  29.                         for (j=i*i;j<=100;j+=i)
  30.                                 nprime[j]=true;
  31.                 }
  32.         ans=0;
  33.         memset(val,-1,sizeof(val));
  34.         for (i=2;i<=10000;i++)
  35.                 if (val[i]==-1)
  36.                 {
  37.                         val[i]=calc(i)-i;
  38.                         if (val[i]<=10000&&val[i]>i)
  39.                         {
  40.                                 val[val[i]]=calc(val[i])-val[i];
  41.                                 if (val[val[i]]==i)
  42.                                 {
  43.                                         ans+=i;
  44.                                         ans+=val[i];
  45.                                 }
  46.                         }
  47.                 }
  48.         printf("%d\n",ans);
  49.         return 0;
  50. }

 

 

Prject Euler Comments(0) 2009年7月22日 05:10

Project Euler——Problem 20

原题与答案：

Problem 20

21 June 2002

n! means n × (n - 1) × ... × 3 × 2 × 1

Find the sum of the digits in the number 100!

Answer:648

 

分析与解答：

题目的意思很明朗，是求100!的各位数字之和，啥都不说了，高精度直接计算即可，提及一下位数的估计，因为100!最坏情况下看成是100个100相乘，也就是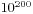10^{200}，不超过201位，当然这还是从多计算，实际上小很多，我的代码中是顺手打了个300意思一下，程序源代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int a[300],i,j,t,ans;
  4. int main()
  5. {
  6.         memset(a,0,sizeof(a));
  7.         a[0]=a[1]=1;
  8.         for (i=1;i<=100;i++)
  9.         {
  10.                 t=0;
  11.                 for (j=1;j<=a[0];j++)
  12.                 {
  13.                         a[j]=a[j]*i+t;
  14.                         t=a[j]/10;
  15.                         a[j]%=10;
  16.                 }
  17.                 while (t)
  18.                 {
  19.                         a[++a[0]]=t%10;
  20.                         t/=10;
  21.                 }
  22.         }
  23.         ans=0;
  24.         for (i=1;i<=a[0];i++) ans+=a[i];
  25.         printf("%d\n",ans);
  26.         return 0;
  27. }

 

 

Prject Euler Comments(0) 2009年7月21日 05:06

Project Euler——Problem 19

原题与答案：

Problem 19

14 June 2002

You are given the following information, but you may prefer to do some research for yourself.

  • 1 Jan 1900 was a Monday.
  • Thirty days has September,
    April, June and November.
    All the rest have thirty-one,
    Saving February alone,
    Which has twenty-eight, rain or shine.
    And on leap years, twenty-nine.
  • A leap year occurs on any year evenly divisible by 4, but not on a century unless it is divisible by 400.

How many Sundays fell on the first of the month during the twentieth century (1 Jan 1901 to 31 Dec 2000)?

Answer:171

 

分析与解答：

原题的意思是告诉了1900年1月1日是星期一，还有31日的月份，二月在闰年29天，平年28天，闰年是指年份被4整除，但是世纪年时必须被400整除的年份。最后根据这些已知的条件求20世纪（1901年1月1日到2000年12月31日）每个月第一天是星期天的数目。这题很简单，直接枚举就能得到解答，但是要注意题目中给定的是1900年1月1日是星期天，要转换为1901年1月1日开始，其实不难，只要加上1900年的天数365对7取余就得到1901年1月1日是星期几了，当然我们用0表示星期天。如下是我的源程序代码：

 

  1. #include<stdio.h>
  2. int days[12]={31,28,31,30,31,30,31,31,30,31,30,31},i,j,ans,cur;
  3. int main()
  4. {
  5.         ans=0;
  6.         cur=(1+365)%7;
  7.         for (i=1901;i<=2000;i++)
  8.                 for (j=0;j<12;j++)
  9.                 {
  10.                         if (cur==0) ans++;
  11.                         cur+=days[j];
  12.                         if (j==1&&(i%400==0||(i%100!=0&&i%4==0))) cur++;
  13.                         cur%=7;
  14.                 }
  15.         printf("%d\n",ans);
  16.         return 0;
  17. }

 

 

Prject Euler Comments(0) 2009年7月21日 04:57

Project Euler——Problem 18

原题与答案：

Problem 18

31 May 2002

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

3
7 5
2 4 6
8 5 9 3

That is, 3 + 7 + 4 + 9 = 23.

Find the maximum total from top to bottom of the triangle below:

75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)

Answer:1074

 

分析与解答：

这个是传说中的数字三角形，是利用动态规划的一个经典题目，题目的意思是求从顶端到底部的一条路径，使得路经的数字的和最大，而路径则是可以从上往下走到其左下或者右下的临近数字。思路最直接的是从上往下执行，但是有一种更好的方法求得，现在介绍这种方法，假设a[i][j]表示以第i行j列为顶点的三角形顶点到底边的最大路径值。对于底边的某个数字，其的最优值必然是本身，那么对于中间的值，我们可以得到动态规划方程：a[i][j]=maxn\{a[i+1][j],a[i+1][j+1]\}(1\leq i \leq n,1\leq j \leq i)。我们最后的目标就是得到顶端的值。当然这个题目如果用这种方式就免不了要先把数字先全部读入结束，如果用另一种方法的话，可以利用滚动数组来减少空间的消耗，我是利用从下往上的方式，这样免去了边界的处理，坐标和方程中略微不同，利用是从0开始的坐标，程序源代码如下所示：

 

  1. /*
  2. 75
  3. 95 64
  4. 17 47 82
  5. 18 35 87 10
  6. 20 04 82 47 65
  7. 19 01 23 75 03 34
  8. 88 02 77 73 07 63 67
  9. 99 65 04 28 06 16 70 92
  10. 41 41 26 56 83 40 80 70 33
  11. 41 48 72 33 47 32 37 16 94 29
  12. 53 71 44 65 25 43 91 52 97 51 14
  13. 70 11 33 28 77 73 17 78 39 68 17 57
  14. 91 71 52 38 17 14 91 43 58 50 27 29 48
  15. 63 66 04 68 89 53 67 30 73 16 69 87 40 31
  16. 04 62 98 27 23 09 70 98 73 93 38 53 60 04 23
  17. */
  18. #include<stdio.h>
  19. int a[15][15],i,j;
  20. int main()
  21. {
  22.         for (i=0;i<15;i++)
  23.                 for (j=0;j<=i;j++)
  24.                         scanf("%d",&a[i][j]);
  25.         for (i=13;i>=0;i--)
  26.                 for (j=0;j<=i;j++)
  27.                         a[i][j]+=a[i+1][j]>a[i+1][j+1]?a[i+1][j]:a[i+1][j+1];
  28.         printf("%d\n",a[0][0]);
  29.         return 0;
  30. }

 

 

Prject Euler Comments(0) 2009年7月21日 04:16

Project Euler——Problem 17

原题与答案：

Problem 17

17 May 2002

If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3 + 3 + 5 + 4 + 4 = 19 letters used in total.

If all the numbers from 1 to 1000 (one thousand) inclusive were written out in words, how many letters would be used?

NOTE: Do not count spaces or hyphens. For example, 342 (three hundred and forty-two) contains 23 letters and 115 (one hundred and fifteen) contains 20 letters. The use of "and" when writing out numbers is in compliance with British usage.

Answer:21124

 

分析与解答：

这个题目是到现在为止最为恶心的题目，是求1到1000所构成的英文单词除掉空格的总长度。当然是可以笔算的，但是最麻烦的是去数单词的长度（我不喜欢英语）。笔算的过程很多种，我介绍一下我自己的吧，首先是1到9的总长度=3+3+5+4+4+3+5+5+4=36，然后是10到19总长度=3+6+6+8+8+7+7+9+8+8=70，接着从20到99都有规律可循了，20到90所有10倍数的单词总长度=6+6+5+5+5+7+6+6=46，而个位都是1到9，于是1到99的总长度=36×9+70+46×10=854。伴随1到999，1到99总是一轮轮出现的，总次数是10次，因此十位和各位总长度=854×10=8540。接下来就是百位了，百位有点麻烦，虽然是1到9数字每个各出现了100次，但是还有单词"hundred"，此外还有"and"，但是不影响计算，百位总长度=36×100+7×900+3×9×99=12573。于是就得到了1到999的总长度=8540+12573=21113。最后加上单词"onethousand"，那么我们得到的答案=21113+11=21114。我的程序稍微偷懒了一下，用了枚举各个位的情况（等于枚举了1到999），累加，源代码如下：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int ans=0,ones[10]={0,3,3,5,4,4,3,5,5,4},tens[10]={0,0,6,6,5,5,5,7,6,6},ten[10]={3,6,6,8,8,7,7,9,8,8},i,j,k;
  4. int main()
  5. {
  6.         for (i=0;i<10;i++)
  7.                 for (j=0;j<10;j++)
  8.                         for (k=0;k<10;k++)
  9.                         {
  10.                                 if (j!=1) ans+=ones[i]+tens[j]+ones[k];
  11.                                 else ans+=ones[i]+ten[k];
  12.                                 if (i) ans+=10;
  13.                                 if (i&&j+k==0) ans-=3;
  14.                         }
  15.         printf("%d\n",ans+strlen("onethousand"));
  16.         return 0;
  17. }

 

 

Prject Euler Comments(0) 2009年7月19日 17:47

Project Euler——Problem 16

原题与答案：

Problem 16

03 May 2002

2^(15) = 32768 and the sum of its digits is 3 + 2 + 7 + 6 + 8 = 26.

What is the sum of the digits of the number 2^(1000)?

Answer:1366

 

分析与解答：

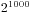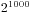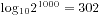这个题目题意很直接，就是求2^{1000}各位数的和，直接的做法就是用高精度乘法直接求得结果，然后进行求和，程序也十分容易编写，2^{1000}的位数是log_{10}2^{1000}=302。程序源代码如下所示：

 

  1. #include<stdio.h>
  2. #include<string.h>
  3. int a[400],i,j,s;
  4. int main()
  5. {
  6.         memset(a,0,sizeof(a));
  7.         a[0]=a[1]=1;
  8.         for (i=1;i<=1000;i++)
  9.         {
  10.                 for (j=1,s=0;j<=a[0];j++)
  11.                 {
  12.                         a[j]=a[j]*2+s;
  13.                         s=a[j]/10;
  14.                         a[j]%=10;
  15.                 }
  16.                 if (s) a[++a[0]]=s;
  17.         }
  18.         for (i=1,s=0;i<=a[0];i++) s+=a[i];
  19.         printf("%d\n",s);
  20.         return 0;
  21. }

 

 

Prject Euler Comments(0) 2009年7月19日 17:41