Project Euler——Problem 29

daybreakcx posted @ 2009年7月27日 18:58 in Prject Euler , 1668 阅读

原题与答案：

Problem 29

25 October 2002

Consider all integer combinations of a^b for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:

2²=4, 2³=8, 2⁴=16, 2⁵=32
3²=9, 3³=27, 3⁴=81, 3⁵=243
4²=16, 4³=64, 4⁴=256, 4⁵=1024
5²=25, 5³=125, 5⁴=625, 5⁵=3125

If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:

4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125

How many distinct terms are in the sequence generated by a^b for 2 ≤ a ≤ 100 and 2 ≤ b ≤100?

Answer:9183

分析与解答：

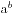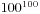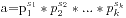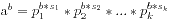题目的意思是由在[2,100]区间中的a和b由 a^b 形式构成的数有多少个。首先我们先确定一点，那就是 $a_1^{b_1}=a_2^{b_2}$ 这样的情况是存在的，比如 2^4=4^2 ，那么也就是说有重复的数值存在，其次是我们是否需要求出每一个数值的具体大小呢？答案是否定的，在[2,100]区间中，我们得到的最大数值是 $100^{100}$ ，大概有201位，直接去算那么数值比较大，而且比较也很久，我们就要想换一种方法。我们利用一个更快的方法来进行，假设a的质因素分解形式是 $a=p_1^{s_1}*p_2^{s_2}*...*p_k^{s_k}$ ，那么 $a^b=p_1^{b*s_1}*p_2^{b*s_2}*...*p_k^{b*s_k}$ ，我们可以将所有的数值都化成质因素分解的形式，这样我们只需要比较对应的次数，而且在100内的素数只有25个，比较的个数比较少。每次我们分解出a的形式，然后对于 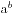a^b 只要将次数都乘以b，就可以了，最后将这些次数序列排个序，计算有多少种即可，我的源程序代码如下所示：

#include<stdio.h>
#include<memory.h>
#include<algorithm>
bool nprime[101];
int a[26],i,j,k,n,ans,temp[25];
struct node
{
int list[25];
}res[9801];
bool cmp(node s,node t)
{
return memcmp(s.list,t.list,sizeof(res[0].list))<0;
}
void calc(int s)
{
int i;
for (i=1;i<=a[0];i++)
{
temp[i-1]=0;
while (s%a[i]==0)
{
s/=a[i];
temp[i-1]++;
}
}
}
int main()
{
a[0]=0;
memset(nprime,false,sizeof(nprime));
for (i=2;i<=100;i++)
if (!nprime[i])
{
a[++a[0]]=i;
if (i<=10)
for (j=i*i;j<=100;j+=i)
nprime[j]=true;
}
n=0;
for (i=2;i<=100;i++)
{
calc(i);
for (j=2;j<=100;j++)
{
for (k=0;k<a[0];k++)
res[n].list[k]=temp[k]*j;
n++;
}
}
std::sort(res,res+n,cmp);
ans=0;
for (i=j=0;;)
{
ans++;
while (j<n&&!memcmp(res[i].list,res[j].list,sizeof(res[0].list))) j++;
if (j==n) break;
i=j;
}
printf("%d\n",ans);
return 0;
}