Project Euler——Problem 30

daybreakcx posted @ 2009年7月27日 20:27 in Prject Euler , 1373 阅读

原题与答案：

Problem 30

08 November 2002

Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:

1634 = 1⁴ + 6⁴ + 3⁴ + 4⁴
8208 = 8⁴ + 2⁴ + 0⁴ + 8⁴
9474 = 9⁴ + 4⁴ + 7⁴ + 4⁴

As 1 = 1⁴ is not a sum it is not included.

The sum of these numbers is 1634 + 8208 + 9474 = 19316.

Find the sum of all the numbers that can be written as the sum of fifth powers of their digits.

Answer:443839

分析与解答：

这个题目的意思是找出所有的等于自己各个位数五次方的和的数（除了1），输出他们的和。题目书写起来很简单，关键难点在于数值范围的判断，因为首先我们的直观想法：如果我们不停的加0，那么数值可以不断变大，但是五次方和不变，同时如果我们加上其他数值，可以调节两者大小关系，貌似这个枚举量是无穷的，但是仔细分析下来，我们得到结论是这个数最多就6位，下面先列出一个表格：

N	0	1	2	3	4	5	6	7	8	9
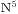	0	1	32	243	1024	3125	7776	16807	32768	59049
0	1	0	-31	-242	-1023	-3124	-7775	-16806	-32767	-59048
1	10	9	-22	-233	-1014	-3115	-7766	-16797	-32758	-59039
2	100	99	68	-143	-924	-3025	-7676	-16707	-32668	-58949
3	1000	999	968	757	-24	-2125	-6776	-15807	-31768	-58049
4	10000	9999	9968	9757	8976	6875	2224	-6807	-22768	-49049
5	100000	99999	99968	99757	98976	96875	92224	83193	67232	40951
6	1000000	999999	999968	999757	998976	996875	992224	983193	967232	940951

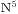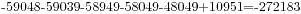首先上面的表格第二行表示 N^5 ，然后下面每行都表示 10^i-N^5 ，换句话说表示的是将数字j固定在i位会对原数减去本位的五次方造成多大的差值。我们的最终结果是在每行取且只取一列使得这些数值的和是0，那么我们如果要让原来数值尽量大，换句话说，如果我们要让数值的位数尽量多，我们就要取负值绝对值较大的，正值绝对值较小的。我们从表中得到我们从低位开始依次要取的数值是9，9，9，9，9，9，9，也就是说当取到6位的时候，不管怎么取，值都是正数，我们先把前5位取9，此时的数值是 -59048-59039-58949-58049-48049+10951=-272183 ，这样就算我们最高位取值是0都会为正数，当然我们最高位不能取0，就取1吧，但不管怎么说，这个数值始终是保持在6位，不可能再大了，因此我们得到了范围后就可以放心枚举了，注意的一点是，最后的结果要把1去掉，我的程序源代码如下：

#include<stdio.h>
#include<string.h>
#include<algorithm>
int ft[10]={0,1,32,243,1024,3125,7776,16807,32768,59049},s,ans,a[6],b[6];
bool get(int s)
{
int i;
for (i=0;i<6;i++)
{
b[i]=s%10;
s/=10;
}
std::sort(b,b+6);
return !memcmp(a,b,sizeof(a));
}
int main()
{
ans=0;
for (a[0]=0;a[0]<=9;a[0]++)
for (a[1]=a[0];a[1]<=9;a[1]++)
for (a[2]=a[1];a[2]<=9;a[2]++)
for (a[3]=a[2];a[3]<=9;a[3]++)
for (a[4]=a[3];a[4]<=9;a[4]++)
for (a[5]=a[4];a[5]<=9;a[5]++)
{
s=ft[a[0]]+ft[a[1]]+ft[a[2]]+ft[a[3]]+ft[a[4]]+ft[a[5]];
if (get(s)) ans+=s;
}
printf("%d\n",ans-1);
return 0;
}