Project Euler——Problem 33

daybreakcx posted @ 2009年8月16日 23:04 in Prject Euler , 1182 阅读

原题与答案：

Problem 33

20 December 2002

The fraction ⁴⁹/₉₈ is a curious fraction, as an inexperienced mathematician in attempting to simplify it may incorrectly believe that ⁴⁹/₉₈ = ⁴/₈, which is correct, is obtained by cancelling the 9s.

We shall consider fractions like, ³⁰/₅₀ = ³/₅, to be trivial examples.

There are exactly four non-trivial examples of this type of fraction, less than one in value, and containing two digits in the numerator and denominator.

If the product of these four fractions is given in its lowest common terms, find the value of the denominator.

Answer:100

分析与解答：

这个题目是说形如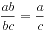 $\dfrac{ab}{bc}=\dfrac{a}{c}$ 的小于1的分数一共有四个，其中ab和bc均为两位数，问这四个分数的乘积的最简分式的分母是什么。这个题目很明显是一个枚举题，这里要用到的就是一个最大公约数的过程，求最大公约数我们可以利用辗转相除法来实现，然后分别依次枚举b,a和c，要注意的是三个数都必须非0，而且c>a，实际上这题的实现很简单，具体的程序源代码如下所示：

#include<stdio.h>
int i,j,k,s,t,num,den;
int gcd(int x,int y)
{
int t;
while (t=x%y)
{
x=y;
y=t;
}
return y;
}
int main()
{
num=den=1;
for (i=1;i<10;i++)
for (j=1;j<10;j++)
for (k=j+1;k<10;k++)
{
s=gcd(j*10+i,i*10+k);
t=gcd(j,k);
if ((j*10+i)/s==j/t&&(i*10+k)/s==k/t)
{
num*=j;
den*=k;
}
}
printf("%d\n",den/gcd(num,den));
return 0;
}