Project Euler——Problem 34

daybreakcx posted @ 2009年8月16日 23:29 in Prject Euler , 1110 阅读

原题与答案：

Problem 34

03 January 2003

145 is a curious number, as 1! + 4! + 5! = 1 + 24 + 120 = 145.

Find the sum of all numbers which are equal to the sum of the factorial of their digits.

Note: as 1! = 1 and 2! = 2 are not sums they are not included.

Answer:40730

分析与解答：

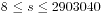这个题目是求除了1和2以外的等于自身各位数值阶乘的和的数，输出他们的和。题目本身的难点在于求范围，因为如果我们需要枚举的数值范围很大的话就要考虑用构造的方法了，所以我们先来判定一下一个n位数他的求值范围是 $n \leq s \leq n*9!$ ，那么我们可以很容易想到那个n位数不可能是无限大的，因为每加上一位，和最大只添加9!=362880，于是通过尝试发现n为8的时候，求值范围是 $8 \leq s \leq 2903040$ ，在最大值只有7位数，明显8位数不在我们的枚举范围之内。同时n为7的时候 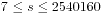$7 \leq s \leq 2540160$ ，还可能存在所求的数值，因此我们枚举的范围最后定下来是 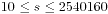$10 \leq s \leq 2540160$ ，自然就得到了如下程序源代码了：

#include<stdio.h>
int fact[10],base[10],i,j,s,ans;
int calc(int s)
{
int ret=0;
while (s)
{
ret+=fact[s%10];
s/=10;
}
return ret;
}
int main()
{
fact[0]=1;
for (i=1;i<=9;i++) fact[i]=fact[i-1]*i;
base[0]=1;
for (i=1;i<=7;i++) base[i]=base[i-1]*10;
for (s=fact[9],i=2;i<=7;i++)
{
s+=fact[9];
for (j=base[i-1];j<base[i]&&j<=s;j++)
if (calc(j)==j) ans+=j;
}
printf("%d\n",ans);
return 0;
}