Learn You a Haskell for Great Good!——(2)起步
这下我们可以开始我们的Haskell之旅了,我们说过Haskell有两种执行的环境,一种是动态脚本语言那种输入即得结果的方式,另一种是编译执行方式。我们闲来进行第一种,与python类似,Haskell也有个相似的环境,我的环境是Fedora 11下GHC 6.10.3,大家要安装的话直接yum即可。我们输入ghci后即可进入我们需要的环境了,显示效果如下:
GHCi, version 6.10.3: http://www.haskell.org/ghc/ :? for help Loading package ghc-prim ... linking ... done. Loading package integer ... linking ... done. Loading package base ... linking ... done. Prelude>
其启动时候载入了一些基本的包,如提示所示,我们可以输入":?"来获得提示,基本上ghci下的命令都是以冒号开头的,具体可以实际查阅。
这里命令行提示符是"Prelude>",当然如果你看的不爽的话可以自己改动,比如Windows控你可以这么改 :
:
Prelude> :set prompt "c:\>" c:\>
我没有这个癖好,所以改不改无所谓,就保持原样了。
平时我们可以将ghci作为一个普通的计算器来玩,比如我们进行如下操作:
Prelude> 5 + 7 12 Prelude> 12 * 14 168 Prelude> 23 - 12 11 Prelude> 4 / 3 1.3333333333333333 Prelude> (1 * 5) - 12 -7 Prelude> 2 * 5 - 17 -7
这里是一些常规的数值计算,符合基本的运算法则,运算的优先级和我们平时的一样,括号用来提升优先级,但是要注意的是如果是一个负数,即带有负号的话,记住一定要加上括号,否则在ghci下会出错,比如:
Prelude> 3 + -2
<interactive>:1:0:
Precedence parsing error
cannot mix `+' [infixl 6] and prefix `-' [infixl 6] in the same infix expression
为什么呢,会造成这个错误的原因是因为不论加减乘除或者是其他运算,其实都是一个函数,如下足矣证明:
Prelude> :info - class (Eq a, Show a) => Num a where ... (-) :: a -> a -> a ... -- Defined in GHC.Num infixl 6 -
这个信息具体的内容是标明了减或者负号是在GHC.Num中定义的,其参数和返回值的形式是a -> a -> a的,其中a是一个数值类型。参数是前两个a,而返回值是最后一个a,我们说过Haskell是可以实现类型推断的,而为什么这里的参数形式不写成(a , a) -> a呢,原因其实也很简单,实际上在Haskell中不管你形式上参数有多少个,实际上一个也没有,比如我们定义了一个函数add a b c = a + b + c,实际上是add = (\a -> (\b -> (\c -> a + b + c)))。而Haskell中函数的调用和C中不同,不用括号和逗号那些,而是直接以空格加以分割,同时Haskell的函数调用是按照模式进行匹配的,匹配上了则进行调用,也就是若将其当做一个参数元素则需要加括号以强调,所以才有上面的现象。
前面反复说过Haskell的类型推断,当然我们也可以看一个表达式的类型(函数实际上可以看成一大堆表达式的叠代,对于惰性的Haskell,最后需要结果的时候才进行计算),比如下面这样:
Prelude> :type (5 + 3) (5 + 3) :: (Num t) => t
说过了数值计算,下面来说说逻辑运算,逻辑基本元有两种,分别是"True"和"False“,分别表示真假,同时基本逻辑运算有与或非分别为&&,||和not,表达式产生逻辑值有等与不等两种,分别用"=="和"/="表示,用法和C中都非常像。下面的几个原文中的试验能大概说明问题:
Prelude> True && False False Prelude> True && True True Prelude> False || True True Prelude> not False True Prelude> not (True && True) False Prelude> 5 == 5 True Prelude> 1 == 0 False Prelude> 5 /= 5 False Prelude> 5 /= 4 True Prelude> "hello" == "hello" True
我们始终需要强调的是Haskell是强制类型的,所以对于一个二元逻辑运算的双方必须是”可比“的,如下会发生错误:
Prelude> 5 == True
<interactive>:1:0:
No instance for (Num Bool)
arising from the literal `5' at :1:0 Possible fix: add an instance declaration for (Num Bool) In the first argument of `(==)', namely `5' In the expression: 5 == True In the definition of `it': it = 5 == True
和C中用0与非0表现假与真不同,Haskell中强调的是类型的模式匹配。所以像上面的表达式是不允许的。
然后再来说说关于一些常用的数值计算吧,除了加减乘除这些以外,Haskell中还有像乘方这些运算。与Python中的乘方(符号是"**")不同,Haskell中的乘方有两种,一种是实数乘方,一种是整数的乘方:
Prelude> 5 ** 80 8.271806125530277e55 Prelude> 5 ^ 80 82718061255302767487140869206996285356581211090087890625
其中前者得到的是一个实数,而后者则是一个整数,Haskell中和Python一样不用管整数的范围,其实本身不用程序员考虑大数值计算,一切已经都办好了。
同时在Haskell中还有一些很好用的函数,如succ,max,min等等,大家可以直接用“:info”命令查一下,试一试。
说完基本用法下面来说说函数的写法。我们说过Haskell的执行方法其实类似于C中的define,是大量的表达式替换,因此Haskell中函数的定义中其特点也很明显,用一个等号来联系函数形式和实体,如原文中的一个函数的定义如下:
doubleMe x = x + x
我们可以将上述内容写成一个拓展名为".hs"文件,如"heihei.hs",类似于我们平时写的一个头文件,然后在ghci中执行":l heihei"就可以调用了,下面是效果:
Prelude> :l heihei [1 of 1] Compiling Main ( heihei.hs, interpreted ) Ok, modules loaded: Main. *Main> doubleMe 5 10 *Main> doubleMe 3.2 6.4
当然如果我们直接在ghci中写函数也是可以的,我们可以用let来进行定义:
Prelude> let doubleMe x = x + x Prelude> doubleMe 5 10 Prelude> doubleMe 3.2 6.4
这里let的使用习惯了C的朋友可以当做是定义变量的方法,比如我们这么做:
Prelude> let a = "heihei" Prelude> a "heihei" Prelude> let b = 1 Prelude> b 1
但是这里本质上不是变量,正如我们所一直强调的,只是表达式的替换,也就是一大堆define语句,而并非C中的变量那样开辟空间,然后赋值调用,而函数的声明同样可以用let这样(let在ghci中用,hs文件中不用)其实也表明了实际上函数也只是表达式替换。如原文中所说的,我们也同样可以用if语句进行分支,如原文中的程序:
doubleSmallNumber' x = (if x > 100 then x else x*2) + 1
至于函数的更为丰富的内容,会在以后的文中继续介绍。
下面如原文中介绍一下Haskell中常用的两种数据结构,列表和元组。
列表我们常用的表达式如下:
Prelude> [1,5,2,4,3] [1,5,2,4,3] Prelude> [2.3,1,4] [2.3,1.0,4.0]
列表的元素必须是同种类型的(对于整数有普通整数和大整数之分,同样在实数和整数之间也可以进行转换,优先按照普通整数到实数的顺序来进行,上面的例子中第二个元素全部被转换为了实数。
不同类型的元素是无法存在于同一个列表中的,比如我们在C中整数和字符可以同一使用,但是在Haskell中却不可以:
Prelude> [3,'a']
<interactive>:1:1:
No instance for (Num Char)
arising from the literal `3' at :1:1 Possible fix: add an instance declaration for (Num Char) In the expression: 3 In the expression: [3, 'a'] In the definition of `it': it = [3, 'a']
实际上字符串在Haskell中是一种特殊的列表,比如我们定义的一个字符串用相应的列表操作同样可以实现效果:
Prelude> "abcdef"!!2 'c'
同时列表中的元素还可以是另一个列表,当然子列表的元素类型也必须是一样的,但长度可以不等。
下面几个例子是常用的列表操作:
Prelude> "abcdef" ++ "ghi" "abcdefghi" Prelude> 'a':"bcde" "abcde" Prelude> "abcdef"!!4 'e'
上述的三个操作依次表示列表的合并,加头元素和取某个序号上的元素(和C一样下表从0开始)。
同时列表还支持比较操作,我们可以比较等,不等,大于,小于,大等于和小等于等等,其比较依据是根据列表的字典序规则:
Prelude> [1,2,3] == [4,5,6] False Prelude> [1,2,3] /= [4,5,6] True Prelude> [1,2,3] > [1,3,3] False Prelude> [1,2,3] < [1,3,3] True Prelude> [1,2,4] >= [1,1,8] True Prelude> [1,2,4] <= [2,1,1] True
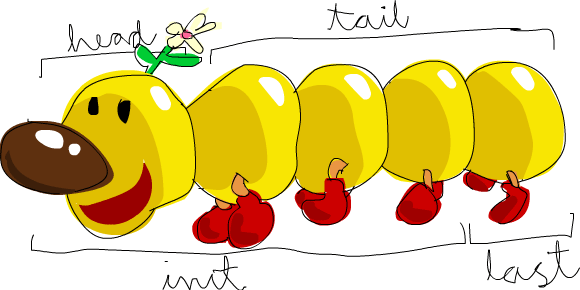
然后便是列表中常用的四个函数了,head,tail,init和last,分别表示首元素,除去首元素列表,除尾元素列表和尾元素:
Prelude> head [1,2,3,4,5] 1 Prelude> tail [1,2,3,4,5] [2,3,4,5] Prelude> init [1,2,3,4,5] [1,2,3,4] Prelude> last [1,2,3,4,5] 5
原文中的那张图片是在太经典使得我忍不住引用一下:
当然,无意义的函数调用是会导致错误的,比如返回空列表的首元素等等,这些在编译中是可以获得的(Haskell太强大了):
Prelude> head [] *** Exception: Prelude.head: empty list
除了上述操作外,列表还有如length,null,reverse,take,drop,maximum,minimum,sum,product和elem等,分别表示求长度,判断是否空,反转,获取元素,去除元素,获取最大值,最小值,求和,乘积和集合元素判断:
Prelude> length [1,2,3] 3 Prelude> null [1,2] False Prelude> reverse [2,5,3,7,4] [4,7,3,5,2] Prelude> take 3 [1,2,3,4,5] [1,2,3] Prelude> drop 2 [1,2,3,4,5] [3,4,5] Prelude> maximum [4,5,1,3,2] 5 Prelude> minimum [4,5,1,3,2] 1 Prelude> sum [4,5,1,3,2] 15 Prelude> product [4,5,1,3,2] 120 Prelude> elem 3 [4,5,1,3,2] True
这里要强调一下elem,实际上elem还可以这么用:
Prelude> 3 `elem` [1,5,3,4] True
这是为了加强可读性而特别实现的,其中的符号是左单引号(键盘键位1左边那个),我们可以这样定义:
Prelude> let a `add` b = a + b Prelude> add 1 2 3 Prelude> 1 `add` 2 3
至于具体细节大家继续自己研究吧,学习这种事情只有自己思考试验得来的才能印象深刻,而且学习的乐趣就在于这些地方了。
说完列表的操作现在来谈谈构造列表,常规模式下我们构造列表可以这么用:
Prelude> [1..20] [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] Prelude> ['a'..'z'] "abcdefghijklmnopqrstuvwxyz" Prelude> ['H'..'Z'] "HIJKLMNOPQRSTUVWXYZ" Prelude> [2,5..18] [2,5,8,11,14,17] Prelude> [2,4..20] [2,4,6,8,10,12,14,16,18,20]
我们可以列出开始元素和结尾元素,而其构造是以等差数列的形式进行的,你可以列前两个元素来确定公差,而最后一个元素定最大元素,终止关系是小等于,大家细细分析上面的例子就知道了,当然如果你喜欢乱试的话前面打上三个元素然后拥有不同的公差,ghci本着恶即斩的原则是不会放过你的:
Prelude> [1,3,7..50] <interactive>:1:6: parse error on input `..'
除了整数和字符,实数不是不可以实现,根据原文的例子我们这么做:
Prelude> [0.1, 0.3 .. 1] [0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999]
这是由于精度造成的,一般我们在C中for循环常常不用实数做循环变量的原因就是这个了,所以建议大家不要轻易使用,仅供参考。
当然还有某些很好用的函数,比如cycle,repeat和replicate,作用分别是重复一个列表组成一个列表,重复元素组成列表和重复一定次数某个元素组成列表,但是最好我们都能加上结束条件,因为Haskell本身是支持无限列表的,如果你打完就回车的话你就等着他刷吧:
Prelude> take 10 (cycle ["Sun.","Mon.","Tues.","Wed.","Thur.","Fri.","Sat."]) ["Sun.","Mon.","Tues.","Wed.","Thur.","Fri.","Sat.","Sun.","Mon.","Tues."] Prelude> take 20 (repeat 5) [5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5] Prelude> replicate 5 10 [10,10,10,10,10]
是不是很开心啊,大家自己试试看吧,很好玩的!
如果你觉得这样还不够自由,不够开心的话,建议你试一下下面这个方法:
Prelude> [x | x <- [1..10], x `mod` 3 == 1] [1,4,7,10]
上面的代码列出了1到10内被3除余1的所有数值,这种方法和Python中的很像,本身的大体思想概括说来是一种集合表示法,'|'符号之前的是集合选取元素表达式,而其后的是集合元素取之范围,至于条件想要加入多少个,看大家自己具体需求了,这里的操作非常的自由,还是老话,大家自己尝试慢慢吧,这里给出一个原文中很经典的例子来供大家欣赏:
Prelude> sum [1 | _ <- [1..20]] 20
这是一个求列表长度的方法,其原则构造一个与原来列表一样长的列表,每个元素都是1,然后求和就可以了,真的很不错啊~至于里头那个下划线是干什么的呢?这个在Haskell中叫做”wild card“,至于怎么翻译我实在找不到一个很好的词,以后看到好的再说吧,其作用是在你的模式中不需要管你取出的元素是什么的情况下就利用wild card来进行替换,你可以在定义函数等地方使用他,这是一个非常实用的技术。
在列表介绍部分结束之前再说些题外话吧,我们平时见到的以中括号圈定的列表表示法其实是一种语法糖,比如列表[1,2,3]其实际的表示形式是1:2:3:[],平时的表示法是为了便于阅读,而我们在函数调用的时候常常会见到如x:xs的形式,其表示列表的首个元素是x,xs是除了x以外的剩余元素,函数的调用是基于模式匹配的,这样调用起来也很方便,大家可以先了解一下,以后遇到了再说。
本章最后的内容是关于元组的,Haskell中的元组用小括号括起来表示,是静态的,基本上可以认为是只读的,这个与Python中的不同,Python中的元组是可变的,比如下面操作:
>>> (1,2)+(3,4) (1, 2, 3, 4)
在Haskell中是不允许的,我们可以构造元组,但是却无法改变元组,二元组的常用操作如下:
Prelude> fst (1, 2) 1 Prelude> snd (1, 2) 2
注意我们所说的是二元组,至于三元组可以不可以用大家试试看就知道了,反正Haskell恶即斩,这种恶行是不会放过的。
前段时间在Haskell群里曾经有人询问如何求一个元组有多少个元素,换句话说获取一个向量的维数,很遗憾这个貌似除了匹配特定有限元组外是无法实现的,因为在Haskell中根本不存在这种操作(至少我现在的知识这么告诉我),你可以去匹配一个元组,可以去获取元组中某一维元素(模式匹配),但是你却没必要知道其有多少维,凡是匹配不上的,就是匹配模式不完全的。
对于元组的构造我们常常用的是zip和zip3,其实这两个函数大家都可以自己写,但是Haskell中为了方便就提供了,其作用为将两个(zip3是三个)列表对应位置上元素组成元组的列表,多说无益,大家看例子:
Prelude> zip [1..] [2,4..20] [(1,2),(2,4),(3,6),(4,8),(5,10),(6,12),(7,14),(8,16),(9,18),(10,20)]
在Haskell无穷列表这类东西便大展拳脚,效果非常的好,很好很强大!此外我们前面的表示法同样适用:
Prelude> [(a, b, c) | a <- [1..10], b <- [1..10], c <- [1..10], a^2 + b^2 == c^2, a <= b] [(3,4,5),(6,8,10)]
这是一个求边长在1到10内的直角三角形边长元组的所有可能情况,很方便吧,这些东西还需大家继续自己尝试,我就不多说什么了,原文中某些例子我也稍微略去,大家有空还是把原文也看一下。
最后说一句:Have Fun!~
 评论 (0)
评论 (0)