Learn You a Haskell for Great Good!——(3)类型与类型类
前面说过Haskell拥有一个静态类型系统,其支持类型推断,可以在编译的时候就确定各类型,对于一个操作(在Haskell中看成一个函数)所不支持的运算均会被编译器查出,这使得程序更为安全,同时很多程序的问题都可以在编译的时候解决,这往往会令反复修改编译的过程变长,但是相比于成品的测试来说,这点付出还是非常值得的。在Haskell中的所有东西都有一个类型,这个很明显地可以利用":type"命令来查看。
与我们见到的如C和Pascal等语言不同,Haskell中不需要显式的变量生命,比如你打入一个数值5.3,Haskell就能推断出这是一个实数,你输入一个[1,2,3,4],Haskell就能知道这是一个列表。类型就像一个表达式的标签一样,告诉我们他与那种事物匹配。通常我们使用":type"命令来获取表达式的类型,如原文中所示:
Prelude> :type 'a' 'a' :: Char Prelude> :type True True :: Bool Prelude> :type "Hello!" "Hello!" :: [Char] Prelude> :type (True, 'a') (True, 'a') :: (Bool, Char) Prelude> :type 4 == 5 4 == 5 :: Bool
通常你可以不用完全打出":type",直接打":t"就可以了,一般情况下ghci中的命令都可以通过取首字母来输入,对于一个类型查看命令,其分为两个部分,第一部分是我们需要查看的表达式,第二部分是其对应的类型,两者用"::"分开。在例子中我们注意到如"Hello!"这样的字符串,实际上是一个Char元素的列表,而对于元组来说,其类型是根据每个元组元素的类型来确定的,比如我们的(True, 'a')其对应的元组类型为(Bool, Char),类型不匹配的元组就是不同的类型,是不可比的,比如我们这么操作:
Prelude> (True, 'a') == (1, 'a')
<interactive>:1:16:
No instance for (Num Bool)
arising from the literal `1' at <interactive>:1:16
Possible fix: add an instance declaration for (Num Bool)
In the expression: 1
In the second argument of `(==)', namely `(1, 'a')'
In the expression: (True, 'a') == (1, 'a')
Prelude> (True, 'a') == (False, 'a')
False
Bool和Num不能算是同一种类型,所以(Bool, Char)和(Num, Char)是无法利用"=="进行比较的。
我们说过,在Haskell中,一切都有其对应的类型,表达式如此,具体数值如此,当然函数也不例外,其实从函数的定义方式我们可以看出在Haskell中函数只是表达式的另一种表现形式,正如我们所说的如C中的define操作一样,其只是不停地叠代,并且到了需要的时候进行计算(惰性)。
如同原文中的函数例子一样,我们常常会见到函数中会有那么一段的类型声明(和用":type"命令输出的一样),虽然Haskell是拥有类型推断的,虽然在一些小型的函数中我们可以省略这个部分而交由编译器来进行处理,但是很多时候我们还是会将这个部分写上的,这是为了方便函数功能的直观认识。原文中的函数是这么定义的:
removeNonUppercase :: [Char] -> [Char] removeNonUppercase st = [ c | c <- st, c `elem` ['A'..'Z']]
我们来读一下函数类型声明部分,这个函数叫做removeNonUppercase,他的输入是一个字符数组,而且输出也是一个字符数组(字符串),这样当我们进行如高阶函数调用等操作的时候,利用":type"来分析一下这个函数的使用方法,调用起来就更为方便了,就如同我们平时在C中从头文件中知道了函数的参数形式一样。
上述例子是一个参数的函数,我们更进一步来看看多个参数的函数是什么形式的:
add :: Int -> Int -> Int -> Int add x y z = x + y + z
这里我们可能会有疑惑,怎么会一下子推导了那么多层,为什么不是我们想象的那样如"Int Int Int -> Int"或者"Int, Int, Int -> Int"这样的形式,刚看这样的形式的时候我很费解,但是后来知道了Haskell下函数的特性后,一切就迎刃而解了,其实这个问题我们讲过,在我的第二篇文章中就提到一个一模一样的例子,当时我说“实际上在Haskell中不管你形式上参数有多少个,实际上都一个也没有,比如我们定义了一个函数add a b c = a + b + c,实际上是add = (\a -> (\b -> (\c -> a + b + c)))“,是的就是这个原因,函数的形式你可以定义多个参数,但是这只是你看到的,对于这个函数而言,对于Haskell而言,本质上只有一个参数,或者说本质上函数名只是一个表达式,而每个参数只是这个表达式的一个部分add = (\a -> (\b -> (\c -> a + b + c)))这个式子很清晰地交代了Int -> Int -> Int -> Int形式的缘由。
如果你给出了一个函数的类型声明,编译器会对其进行检查,如果你没有给出,由于Haskell本身是可类型推断的,所以不影响函数的查看与调用,我们利用":type"命令都可以看到我们想要的结果,这里就有一个问题了,Haskell到底支持哪些基本的类型?原文中将其列出来了。
普通整数(Int):
与C中的int等价,就是一个普通的整数,在32位机上其最大值是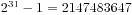 ,最小值是
,最小值是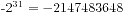
大整数(Integer):
这种整数和普通整数的区别在于其是个高精度整数,其数值范围可以非常的大而不受机器位长的限制,Python中的整数就是这样的,那它受什么限制,抑或是无限呢?如果真的要说的话应该是收到内存限制,在C中我们自己也可以构造这种整数,比如我们用一个char数组来存储一个整数,每个位存储一个整数的一位或者多位,换句话说就是用空间换表达范围,Haskell和Python中这种整数你可以随便使用(必须是整数),但是C中你想用的话就得自己去写了,有时间我再介绍一下高精度运算吧。
单精度浮点数(Float)与双精度浮点数(Double):
这里将两者一起说了,实际上两者和C中的float和double是一样的,都是对于实数的表示,至于浮点数存储格式那些的大家可以自己去查标准,这里不展开。一般来说,我们用的都是Double,如果你想说空间占用或者是计算效率那些的那是具体的实际问题,不在这里的讨论范围之内。一般Double可以提供比Float更多的有效位和更大的表示范围。
布尔类型(Bool):
这个相信大家一定不会陌生,C++中的bool,Pascal中的Boolean,都是这种东西,C99中也加入了布尔类型的变量,虽然平时我们可以利用整形数值的”0“与”非0“表示”假“与“真”,但是C99中加了我们就用吧,反正以前是没有布尔类型但是有布尔概念,逻辑运算照样用,现在默认提供了,就是_Bool,大家就安心吧。言归正传,Haskell中的布尔类型有两个取值,分别是True和False,这个就不再多说了。
字符类型(Char):
这个还是用C来比较,C中的char就是很好的等价物,反正就是用右单引号标注的字符,该怎么用就怎么用。
这里多说几句,在Haskell中平常看到的列表或者元组抑或是结构体都是基本数据类型拼装起来的,而这些东西的命名都是以大写字母开头的(上述六种类型的类型名都是大写字母开头,结构体那些也是),这个和函数名不同,我们见到的函数名都没有以大写字母开头,实际上如果你想以大写字母开头,编译器也不会放你通过,比如我们定义一个函数:
Prelude> let Myadd x y = x + y <interactive>:1:4: Not in scope: data constructor `Myadd'
看见了吗,直接被识别为了一种数据构造子,因此我们以后的函数名大家都注意别以大写字母开头,否则查错的时候不知道这点会让你烦死。
我们在使用“:type”命令的时候常常会见到这种形式:
Prelude> :t head head :: [a] -> a
这里会让我们疑惑,a是什么东西?不像是基本的数据类型,我们联系所对应的函数功能就能猜出一二了,head的功能是取出一个列表的第一个元素,而这里"[a] -> a"如果我们换成"[Char] -> Char"或者是"[Int] -> Int"我们都能看懂,但是实际上head针对的不单纯是整数或者是字符列表,其使用范围更广,可以说是对于所有类型列表都通用(除非是空的),对应各种类型分别写对应的head是不现实的,因为类型是无限的(如不同类型排列的元组),所以我们就引入了一个称为类型变量的东西,也就是说这里a表示着”某种类型“的意思,"[a] -> a"同时也传达着输入一个a类型的列表就要返回一个a类型的元素的意义,而不是其他b或者c类型的元素。我们有a同样可以有b与c,字母表可以不断列下去,一个字母不够了可以用两个(估计也用不到那么多),但是其表示的意思都是为了区分不同的类型:
Prelude> :t fst fst :: (a, b) -> a
a和b可以是同类型的,但是如”(a, b) -> a“则强烈地表达出了返回类型必须与元组的首个元素类型相同的意思。
接下来我们说今天的最后一个内容:类型类。听起来和面向对象有点什么关系,实际上是的。我们曾经说过在Haskell中所有的东西都有类型,当然操作符也不例外,比如我们这么操作查看:
Prelude> :t (==) (==) :: (Eq a) => a -> a -> Bool
操作符的类型是两个同类型的元素到一个布尔型元素,实际上其本身就是一个函数,而且是置于中缀表达式之中的,相类似的还有+-*/这些的,查看他们类型的时候需要用括号将其括起来才可,否则有什么情况大家可以自己去试试看。我们来解释类型类,对于操作符==,我们必须保证其两个操作数必须同时属于Eq这个类型类,也就是说他们必须同时属于一个类型类(Eq)中才是可比的,可比较相等的类型必然是属于Eq类型类之中的。同样使用Eq这个类型类元素的还有如elem这样的函数:
Prelude> :t elem elem :: (Eq a) => a -> [a] -> Bool
看到了吗?同样具有(Eq a)这个部分,这里还有个问题,那个”=>“是什么符号,以前没有出现过!他叫什么名字我不知道,但是它的左边部分称为类型约束,表示函数的参数都必须同时属于符号左边的类型类之中。我们将上面的式子这么看:elem函数取一个类型和另一个此类型对应的列表作为参数,返回一个布尔值,而那个类型必须属于Eq这个类型类之中”。
原文中介绍了几个基本的类型类:
Eq:
如我们上头的例子介绍的,Eq类型类用来支持相等判定,其常用的操作有“==”和“/=”。
Ord:
这个类型类是用来支持大小判定的,常用的操作有“>”,“<”,“>=”和“<=”。这里又涉及了一种称为Ordering的基本类型,其拥有三个基本的常量:GT,LT和EQ,分别表示大于,小于和等于,一般我们用compare函数就可以获得:
Prelude> "Hello" `compare` "World" LT Prelude> compare 5 1 GT Prelude> [1,2,3] `compare` [1,2,3] EQ
这里compare的用法和elem的类似,都额外支持中缀表达式,当然是要现在函数名前后各加上左单引号了(1左边的那个键)。
Show:
如Show这个单词所表示的意思,这个类型类是用来支持将其成员字符串化的,有点类似于C中sprintf的效果,比如我们若下操作的效果:
Prelude> show (5 + 2) "7" Prelude> show pi "3.141592653589793" Prelude> show True "True" Prelude> show 2.1 "2.1"
Read:
这个类型类是和Show的作用相反的,其将一个字符串转换为对应Read支持的成员。这个类型类要特别强调一下,因为其涉及到某些如C中类型转换的问题,一般情况下,我们利用read函数进行如下操作都如我们所预料地返回结果:
Prelude> read "True" || False True Prelude> read "8.2" + 3.8 12.0 Prelude> read "5" - 2 3 Prelude> read "[1,2,3,4]" ++ [3] [1,2,3,4,3]
但是有些时候事情就不像我们想象的那么顺利了:
Prelude> read "4"
<interactive>:1:0:
Ambiguous type variable `a' in the constraint:
`Read a' arising from a use of `read' at <interactive>:1:0-7
Probable fix: add a type signature that fixes these type variable(s)
原因错误提示中说的很明白了,ghci不知道我们需要返回什么,由于”4“可以是一个整数或者一个实数,我们并没有把我们的需求说明,因此当我们需要转换单一元素的时候,最好交代清楚我们的需求,才可以得到编译器的认可:
Prelude> read "5" :: Int 5 Prelude> read "5" :: Float 5.0 Prelude> (read "5" :: Float) * 4 20.0 Prelude> read "[1,2,3,4]" :: [Int] [1,2,3,4] Prelude> read "(3, 'a')" :: (Int, Char) (3,'a')
利用"::"来标明我们想要得到的类型就能让read返回我们需要的值了。
Enum:
从字面上Enum是单词 enumerate的缩写,其表示的意思就是枚举,那么这个类型类支持的就是枚举操作了,而我们常规情况下一般是有序的元素是可顺序枚举的,比如数值(字符是以ASCII码形式体现顺序的,本质上也算数值),原文中有如下例子:
Prelude> ['a'..'e'] "abcde" Prelude> [LT .. GT] [LT,EQ,GT] Prelude> [3 .. 5] [3,4,5] Prelude> succ 'B' 'C'
这就是我们平常做的枚举操作,原文中也列出了LT,EQ和GT的顺序,他们也是可比的,比如我们比较LT和EQ:
Prelude> LT < EQ True
Bounded:
这个类型类所支持的是对于边界的界定,用命令查阅Bounded类型类,如下所示:
Prelude> maxBound :: Bool True Prelude> maxBound :: (Bool, Int, Char, Ordering) (True,2147483647,'\1114111',GT) Prelude> minBound :: (Bool, Int, Char, Ordering) (False,-2147483648,'\NUL',LT)
但是如果你用maxBound来查看Float等便会出错,具体他支持哪些可用":info Bounded"来查看。
Num:
这是个数值类型类,一般的数值都是这个类中,我们见到的某些函数中参数的类型有时候标注上Num就是因为需要的参数必须是数值类型的:
Prelude> :t (*) (*) :: (Num a) => a -> a -> a
比如我们查看一个数值的类型:
Prelude> :t 5 5 :: (Num t) => t
我们可以通过":info Num"命令来查看Num类型类:
Prelude> :info Num class (Eq a, Show a) => Num a where (+) :: a -> a -> a (*) :: a -> a -> a (-) :: a -> a -> a negate :: a -> a abs :: a -> a signum :: a -> a fromInteger :: Integer -> a -- Defined in GHC.Num instance Num Int -- Defined in GHC.Num instance Num Integer -- Defined in GHC.Num instance Num Double -- Defined in GHC.Float instance Num Float -- Defined in GHC.Float
其中包括其支持的操作,同时标明其中的四个实例:Int,Integer,Double和Float。为了加入Num,其必须首先是Eq和Show类型类的友元。
Integral和Floating:
这两个类型类同样也是数值类型类,前者支持整数类型Int和Integer,后者是支持浮点数类型Float和Double。当然我们有时候会看到Fractional类型类,其也是支持浮点数的,但是其支持的符号运算只有”/“,剩下的是两个基本函数recip和fromRational,具体细节可以自己去info,这里列出一个现象比如:
Prelude> :t 20.2 20.2 :: (Fractional t) => t Prelude> :t pi pi :: (Floating a) => a
原文中提出了一个非常有用的函数,叫做fromIntegral,其作用可以通过type查出:
Prelude> :t fromIntegral fromIntegral :: (Integral a, Num b) => a -> b
即将一个整数值变为一个更为普遍的Num,这一般用于类型转换之中,比如我们这么用:
Prelude> length [1..20] + 3.2
<interactive>:1:17:
No instance for (Fractional Int)
arising from the literal `3.2' at <interactive>:1:17-19
Possible fix: add an instance declaration for (Fractional Int)
In the second argument of `(+)', namely `3.2'
In the expression: length ([1 .. 20]) + 3.2
In the definition of `it': it = length ([1 .. 20]) + 3.2
Prelude> fromIntegral (length [1..20]) + 3.2
23.2
length返回的是一个整数值,而在Haskell中整数和实数是无法直接相加的,所以我们利用了一个fromIntegral函数将其转化成更为普遍的Num后就可以加入与实数的加法运算了。
文章末了还是那句话:Have Fun!~~
 评论 (0)
评论 (0)